题目内容
在命题p的四种形式(原命题、逆命题、否命题、逆否命题)中,正确命题的个数记为f(p),已知命题p:“若两条直线l1:a1x+b1y+c1=0,l2:a2x+b2y+c2=0平行,则a1b2-a2b1=0”.那么f(p)=
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:两条直线平行时,一定可以得到a1b2-a2b1=0成立,反过来不一定成立,又有原命题与逆否命题具有相同的真假性,逆命题和否命题具有相同的真假性,得到正确命题是2个,即可得答案.
解答:∵命题p:“若两条直线l1:a1x+b1y+c1=0,
l2:a2x+b2y+c2=0平行,则a1b2-a2b1=0”
原命题是一个真命题,
它的逆命题是:”若a1b2-a2b1=0,则两条直线l1:a1x+b1y+c1=0,
l2:a2x+b2y+c2=0平行”,
这个命题不正确,因为除去平行还有一种关系就是重合,
∴逆命题不正确.
根据原命题与逆否命题具有相同的真假性,得到逆否命题正确,
根据逆命题和否命题具有相同的真假性,得到否命题不正确,
总上可知有2个命题正确,
∴f(p)=2,
故选B.
点评:本题考查四种命题的真假关系,考查四种命题的写法,本题考查两条直线平行的充要条件,本题不需要运算,是一个基础题.
分析:两条直线平行时,一定可以得到a1b2-a2b1=0成立,反过来不一定成立,又有原命题与逆否命题具有相同的真假性,逆命题和否命题具有相同的真假性,得到正确命题是2个,即可得答案.
解答:∵命题p:“若两条直线l1:a1x+b1y+c1=0,
l2:a2x+b2y+c2=0平行,则a1b2-a2b1=0”
原命题是一个真命题,
它的逆命题是:”若a1b2-a2b1=0,则两条直线l1:a1x+b1y+c1=0,
l2:a2x+b2y+c2=0平行”,
这个命题不正确,因为除去平行还有一种关系就是重合,
∴逆命题不正确.
根据原命题与逆否命题具有相同的真假性,得到逆否命题正确,
根据逆命题和否命题具有相同的真假性,得到否命题不正确,
总上可知有2个命题正确,
∴f(p)=2,
故选B.
点评:本题考查四种命题的真假关系,考查四种命题的写法,本题考查两条直线平行的充要条件,本题不需要运算,是一个基础题.

练习册系列答案
相关题目
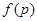 ,已知命题p:“若两条直线
,已知命题p:“若两条直线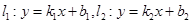 平行,则
平行,则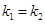 ”。那么
”。那么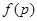 ,已知命题p:“若两条直线
,已知命题p:“若两条直线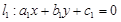 ,
,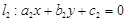 平行,则
平行,则 ”.那么
”.那么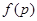 ,已知命题p:“若两条直线
,已知命题p:“若两条直线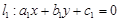 ,
,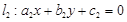 平行,则
平行,则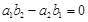 ”.那么
”.那么