题目内容
设椭圆 =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )A.圆x2+y2=2内
B.圆x2+y2=2上
C.圆x2+y2=2外
D.以上三种情况都有可能
【答案】分析:先根据x1+x2=-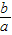 ,x1x2=-
,x1x2=-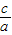 表示出x12+x22,再由e=
表示出x12+x22,再由e=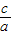 =
= 得到a与c的关系,从而可表示出b与c的关系,然后代入到x12+x22的关系式中可得到x12+x22的范围,从而可确定答案.
得到a与c的关系,从而可表示出b与c的关系,然后代入到x12+x22的关系式中可得到x12+x22的范围,从而可确定答案.
解答:解:∵x1+x2=-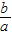 ,x1x2=-
,x1x2=-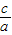
x12+x22=(x1+x2)2-2x1x2=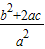
e=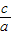 =
= ∴a=2c
∴a=2c
b2=a2-c2=3c2
所以x12+x22=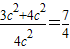 <2
<2
所以在圆内
故选A.
点评:本题主要考查椭圆的基本性质的应用.考查对椭圆基础知识的综合应用.
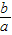 ,x1x2=-
,x1x2=-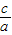 表示出x12+x22,再由e=
表示出x12+x22,再由e=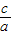 =
= 得到a与c的关系,从而可表示出b与c的关系,然后代入到x12+x22的关系式中可得到x12+x22的范围,从而可确定答案.
得到a与c的关系,从而可表示出b与c的关系,然后代入到x12+x22的关系式中可得到x12+x22的范围,从而可确定答案.解答:解:∵x1+x2=-
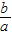 ,x1x2=-
,x1x2=-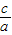
x12+x22=(x1+x2)2-2x1x2=
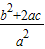
e=
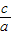 =
= ∴a=2c
∴a=2cb2=a2-c2=3c2
所以x12+x22=
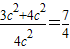 <2
<2所以在圆内
故选A.
点评:本题主要考查椭圆的基本性质的应用.考查对椭圆基础知识的综合应用.

练习册系列答案
相关题目
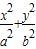 =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( ) =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )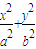 =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )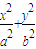 =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )