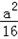题目内容
某养殖场靠墙要编制一条总长度为a的矩形篱笆(靠墙一边不用篱笆),那么所围成的矩形面积的最大值为
- A.

- B.

- C.

- D.

C
分析:设不平行于墙的一边长为x,则另一边长为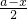 ,表示出矩形面积,再利用基本不等式可求的矩形面积的最大值.
,表示出矩形面积,再利用基本不等式可求的矩形面积的最大值.
解答:设不平行于墙的一边长为x,则另一边长为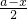
∴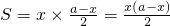 =
=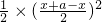 =
=
当且仅当x=a-x时,围成的矩形面积的最大值为
故选C.
点评:本题考查函数模型的构建,考查基本不等式的运用,属于基础题.
分析:设不平行于墙的一边长为x,则另一边长为
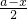 ,表示出矩形面积,再利用基本不等式可求的矩形面积的最大值.
,表示出矩形面积,再利用基本不等式可求的矩形面积的最大值.解答:设不平行于墙的一边长为x,则另一边长为
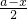
∴
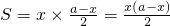 =
=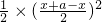 =
=
当且仅当x=a-x时,围成的矩形面积的最大值为

故选C.
点评:本题考查函数模型的构建,考查基本不等式的运用,属于基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目