题目内容
甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为b,乙能攻克的概率为c,丙能攻克的概率为z=(b-3)2+(c-3)2.
(Ⅰ)求这一技术难题被攻克的概率;
(Ⅱ)现假定这一技术难题已被攻克,上级决定奖励z=4万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金x2-bx-c=0万元;若只有2人攻克,则奖金奖给此二人,每人各得a∈1,2,3,4万元;若三人均攻克,则奖金奖给此三人,每人各得
万元.设甲得到的奖金数为X,求X的分布列和数学期望.
(Ⅰ)求这一技术难题被攻克的概率;
(Ⅱ)现假定这一技术难题已被攻克,上级决定奖励z=4万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金x2-bx-c=0万元;若只有2人攻克,则奖金奖给此二人,每人各得a∈1,2,3,4万元;若三人均攻克,则奖金奖给此三人,每人各得
| a | 3 |
分析:(I)根据所给的条件知,甲、乙、丙三人独立地,这是一个相互独立事件同时发生的概率,正面解决比较麻烦,需要从对立事件来解决,能够攻克的对立事件是都不能攻克.
(II)由题意得到变量的可能取值,结合变量对应的事件和条件概率的公式,求出每一个变量的概率,写出分布列,做出期望值.
(II)由题意得到变量的可能取值,结合变量对应的事件和条件概率的公式,求出每一个变量的概率,写出分布列,做出期望值.
解答:解:(Ⅰ)由题意知这一个技术被攻克的对立事件是三个人都没有攻克,
所求事件的概率P=1-(1-
)(1-
)[1-
]=
(II)由题意知X的可能取值是0,
,
,a
P(X=0)=
=
,P(X=
)=
=
P(X=
)=
=
,P(X=a)=1-
-
-
=
∴X的分布列是
∴EX=0×
+
×
+
×
+a×
=
所求事件的概率P=1-(1-
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 24 |
| 60 |
(II)由题意知X的可能取值是0,
| a |
| 3 |
| a |
| 2 |
P(X=0)=
| ||||||
|
| 19 |
| 59 |
| a |
| 3 |
| ||||||
|
| 24 |
| 59 |
P(X=
| a |
| 2 |
| ||||||||||
|
| 14 |
| 59 |
| 19 |
| 59 |
| 24 |
| 59 |
| 14 |
| 59 |
| 2 |
| 59 |
∴X的分布列是
| X | 0 |
|
|
a | ||||||||
| P |
|
|
|
|
| 19 |
| 59 |
| a |
| 3 |
| 24 |
| 59 |
| a |
| 2 |
| 14 |
| 59 |
| 2 |
| 59 |
| 17a |
| 59 |
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是数字的运算比较麻烦,需要认真计算,得到结果.
本题需要改正:甲能攻克的概率为3分之1,乙能攻克的概率为4分之1,丙能攻克的概率为z=5分之1.
(Ⅰ)求这一技术难题被攻克的概率;
(Ⅱ)现假定这一技术难题已被攻克,上级决定奖励a万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金;若只有2人攻克,则奖金奖给此二人,每人各得一半;若三人均攻克,则奖金奖给此三人,每人各得
万元.设甲得到的奖金数为X,求X的分布列和数学期望.
本题需要改正:甲能攻克的概率为3分之1,乙能攻克的概率为4分之1,丙能攻克的概率为z=5分之1.
(Ⅰ)求这一技术难题被攻克的概率;
(Ⅱ)现假定这一技术难题已被攻克,上级决定奖励a万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金;若只有2人攻克,则奖金奖给此二人,每人各得一半;若三人均攻克,则奖金奖给此三人,每人各得
| a |
| 3 |

练习册系列答案
相关题目
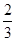 ,乙能攻克的概率为
,乙能攻克的概率为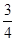 ,丙能攻克的概率为
,丙能攻克的概率为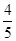 .
.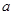 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金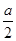 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得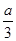 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分) 万元.设甲得到的奖金数为X,求X的分布列和数学期望.
万元.设甲得到的奖金数为X,求X的分布列和数学期望.