题目内容
已知不等式x2-3x+t<0的解集为{x|1<x<m,x∈R}。
(I)求t,m的值;
(Ⅱ)若函数f(x)=-x2+ax+4在区间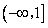 上递增,求关于x的不等式loga(-mx2+3x+2-t)<0的解集。
上递增,求关于x的不等式loga(-mx2+3x+2-t)<0的解集。
(I)求t,m的值;
(Ⅱ)若函数f(x)=-x2+ax+4在区间
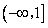 上递增,求关于x的不等式loga(-mx2+3x+2-t)<0的解集。
上递增,求关于x的不等式loga(-mx2+3x+2-t)<0的解集。 解:(Ⅰ)∵不等式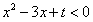 的解集为
的解集为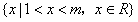 ,
,
∴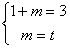 ,解得
,解得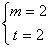 。
。
(Ⅱ)∵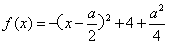 在
在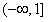 上递增,
上递增,
∴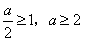 ,
,
又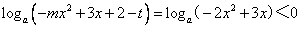 ,
,
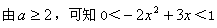 ,
,
由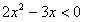 ,得0<x<
,得0<x<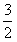 ;
;
由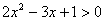 ,得x<
,得x<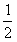 或x>1,
或x>1,
故原不等式的解集为{x|0<x<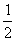 或1<x<
或1<x<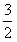 }。
}。
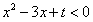 的解集为
的解集为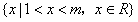 ,
,∴
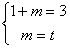 ,解得
,解得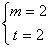 。
。(Ⅱ)∵
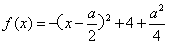 在
在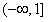 上递增,
上递增,∴
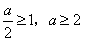 ,
,又
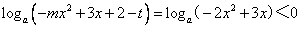 ,
,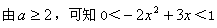 ,
,由
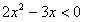 ,得0<x<
,得0<x<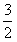 ;
;由
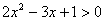 ,得x<
,得x<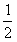 或x>1,
或x>1, 故原不等式的解集为{x|0<x<
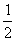 或1<x<
或1<x<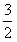 }。
}。 
练习册系列答案
相关题目