题目内容
已经三角形的三边分别是整数l,m,n,且l>m>n,已知{| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
分析:根据{
}={
}={
},可知3l、3m、3n的末四位数字相同即求满足3l°3m≡3n( mod 104)的l、m、n,利用取余以及数的分析,即可求得结论.
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
解答:解:∵{
}={
}={
},∴3l、3m、3n的末四位数字相同,,
即求满足3l°3m≡3n( mod 104)的l、m、n.∴3n(3l-n-1)≡0 (mod 104).(l-n>0)
但 (3n,104)=1,故必有3l-n≡1(mod 104);同理3m-n≡1(mod 104).
下面先求满足3x≡1(mod 104)的最小正整数x.
∵j(104)=104??=4000.故x|4000.用4000的约数试验:
∵x=1,2,时3x1(mod 10),而34≡1(mod 10),∴x必须是4的倍数;
∵x=4,8,12,16时3x1(mod 102),而320≡1(mod 102),∴x必须是20的倍数;
∵x=20,40,60,80时3x1(mod 103),而3100≡1(mod 103),∴x必须是100的倍数;
∵x=100,200,300,400时3x1(mod 104),而3500≡1(mod 104).
即,使3x≡1(mod 104)成立的最小正整数x=500,从而l-n、m-n都是500的倍数,
设l-n=500k,m-n=500h,(k,h∈N*,k>h).
由m+n>l,即n+500h+n>n+500k,?n>500(k-h)≥500,故n≥501.
取n=501,m=1001,l=1501,即为满足题意的最小三个值.
∴所求周长的最小值为3003.
故答案为3003.
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
即求满足3l°3m≡3n( mod 104)的l、m、n.∴3n(3l-n-1)≡0 (mod 104).(l-n>0)
但 (3n,104)=1,故必有3l-n≡1(mod 104);同理3m-n≡1(mod 104).
下面先求满足3x≡1(mod 104)的最小正整数x.
∵j(104)=104??=4000.故x|4000.用4000的约数试验:
∵x=1,2,时3x1(mod 10),而34≡1(mod 10),∴x必须是4的倍数;
∵x=4,8,12,16时3x1(mod 102),而320≡1(mod 102),∴x必须是20的倍数;
∵x=20,40,60,80时3x1(mod 103),而3100≡1(mod 103),∴x必须是100的倍数;
∵x=100,200,300,400时3x1(mod 104),而3500≡1(mod 104).
即,使3x≡1(mod 104)成立的最小正整数x=500,从而l-n、m-n都是500的倍数,
设l-n=500k,m-n=500h,(k,h∈N*,k>h).
由m+n>l,即n+500h+n>n+500k,?n>500(k-h)≥500,故n≥501.
取n=501,m=1001,l=1501,即为满足题意的最小三个值.
∴所求周长的最小值为3003.
故答案为3003.
点评:此题属与难题.考查指数函数的综合应用和取余以及对数的分析,要求基础理论要扎实,是一道竞赛题,好题.

练习册系列答案
相关题目
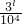 }={
}={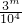 }={
}={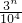 },其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为________.
},其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为________. }={
}={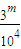 }={
}={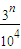 },其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为 .
},其中{x}=x-[x],而[x]表示不超过x的最大整数.则这种三角形周长的最小值为 .