题目内容
已知双曲线C的一条渐近线为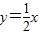 ,且与椭圆
,且与椭圆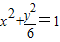 有公共焦点.
有公共焦点.(1)求双曲线C的方程;
(2)直线
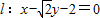 与双曲线C相交于A,B两点,试判断以AB为直径的圆是否过原点,并说明理由.
与双曲线C相交于A,B两点,试判断以AB为直径的圆是否过原点,并说明理由.
【答案】分析:(1)确定椭圆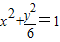 的焦点坐标,设双曲线的方程为:
的焦点坐标,设双曲线的方程为: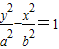 (a>0,b>0),利用双曲线C的一条渐近线为
(a>0,b>0),利用双曲线C的一条渐近线为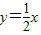 ,且与椭圆
,且与椭圆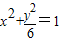 有公共焦点,即可求得双曲线的方程;
有公共焦点,即可求得双曲线的方程;
(2)直线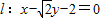 与双曲线C联立,消元,可证明:xAxB+yAyB=0,即可证得以AB为直径的圆过原点.
与双曲线C联立,消元,可证明:xAxB+yAyB=0,即可证得以AB为直径的圆过原点.
解答:解:(1)椭圆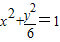 的焦点坐标为(0,±
的焦点坐标为(0,±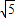 )
)
设双曲线的方程为: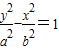 (a>0,b>0),则
(a>0,b>0),则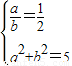 ,∴a=1,b=2
,∴a=1,b=2
∴双曲线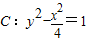 ;
;
(2)直线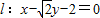 与双曲线C联立,消元可得
与双曲线C联立,消元可得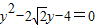
∴yAyB=-4,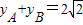
∴xAxB=2yAyB+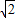 (yA+yB)+4=4
(yA+yB)+4=4
∴xAxB+yAyB=0
∴OA⊥OB
∴以AB为直径的圆过原点.
点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,联立方程,运用韦达定理是关键.
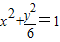 的焦点坐标,设双曲线的方程为:
的焦点坐标,设双曲线的方程为: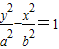 (a>0,b>0),利用双曲线C的一条渐近线为
(a>0,b>0),利用双曲线C的一条渐近线为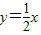 ,且与椭圆
,且与椭圆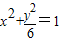 有公共焦点,即可求得双曲线的方程;
有公共焦点,即可求得双曲线的方程;(2)直线
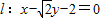 与双曲线C联立,消元,可证明:xAxB+yAyB=0,即可证得以AB为直径的圆过原点.
与双曲线C联立,消元,可证明:xAxB+yAyB=0,即可证得以AB为直径的圆过原点.解答:解:(1)椭圆
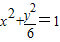 的焦点坐标为(0,±
的焦点坐标为(0,±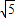 )
)设双曲线的方程为:
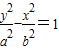 (a>0,b>0),则
(a>0,b>0),则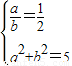 ,∴a=1,b=2
,∴a=1,b=2∴双曲线
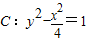 ;
;(2)直线
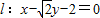 与双曲线C联立,消元可得
与双曲线C联立,消元可得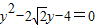
∴yAyB=-4,
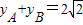
∴xAxB=2yAyB+
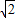 (yA+yB)+4=4
(yA+yB)+4=4∴xAxB+yAyB=0
∴OA⊥OB
∴以AB为直径的圆过原点.
点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,联立方程,运用韦达定理是关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
