题目内容
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为
,
,
,乙队每人答对的概率都是
.设每人回答正确与否相互之间没有影响,用ξ表示甲队总得分.
(Ⅰ)求随机变量ξ的分布列及其数学期望E(ξ);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
(Ⅰ)求随机变量ξ的分布列及其数学期望E(ξ);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
分析:(Ⅰ)由题设知ξ的可能取值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出随机变量ξ的分布列和数学期望E(ξ).
(Ⅱ)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B,分别求出P(A),P(AB),再由P(B/A)=
,能求出结果.
(Ⅱ)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B,分别求出P(A),P(AB),再由P(B/A)=
| P(AB) |
| P(A) |
解答:解:(Ⅰ)由题设知ξ的可能取值为0,1,2,3,
P(ξ=0)=(1-
)(1-
)(1-
)=
,
P(ξ=1)=
(1-
)(1-
)+(1-
)×
×(1-
)+(1-
)(1-
)×
=
,
P(ξ=2)=
×
×(1-
)+
×(1-
)×
+(1-
)×
×
=
,
P(ξ=3)=
×
×
=
,
∴随机变量ξ的分布列为:
数学期望E(ξ)=0×
+1×
+2×
+3×
=
.
(Ⅱ)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B,
则P(A)=
×
×(
)3+
×
×(
)2×(1-
)+
×
×
×(1-
)2=
,
P(AB)=
×
×
×(1-
)2=
,
P(B|A)=
=
=
.
P(ξ=0)=(1-
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 24 |
P(ξ=1)=
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=2)=
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 11 |
| 24 |
P(ξ=3)=
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
∴随机变量ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 24 |
| 1 |
| 4 |
| 11 |
| 24 |
| 1 |
| 4 |
| 23 |
| 12 |
(Ⅱ)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B,
则P(A)=
| 1 |
| 4 |
| C | 3 3 |
| 2 |
| 3 |
| 11 |
| 24 |
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| C | 1 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
P(AB)=
| 1 |
| 4 |
| C | 1 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 18 |
P(B|A)=
| P(AB) |
| P(A) |
| ||
|
| 1 |
| 6 |
点评:本题考查离散型随机变量的期分布列和数学期望,考查条件概率的求法,是历年高考的必考题型之一,解题时要注意排列组合知识的合理运用.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,乙队每人答对的概率都是
,乙队每人答对的概率都是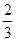 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用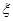 表示甲队总得分.
表示甲队总得分.