题目内容
14.设实数m,n满足m>0,n<0,且$\frac{1}{m}+\frac{1}{n}=1$,则4m+n( )| A. | 有最小值9 | B. | 有最大值9 | C. | 有最大值1 | D. | 有最小值1 |
分析 通过“1”的代换,利用基本不等式求解表达式的最值,判断选项即可.
解答 解:因为$\frac{1}{m}+\frac{1}{n}=1$,所以4m+n=(4m+n)($\frac{1}{m}+\frac{1}{n}$)=5+$\frac{4m}{n}+\frac{n}{m}$.
又m>0,n<0,所以$-\frac{4m}{n}-\frac{n}{m}$≥4,当且仅当n=2m时取等号,故5+$\frac{4m}{n}+\frac{n}{m}$≤5-4=1.
当且仅当$m=\frac{1}{2},n=-1$时取等号.
故选C.
点评 本题考查基本不等式的应用,函数的最值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.对于任意实数x,规定[x]表示不大于x的最大整数,则不等式4[x]2-12[x]+5<0成立的充分不必要条件是( )
| A. | x∈($\frac{1}{2}$,$\frac{5}{2}$) | B. | x∈($\frac{1}{2}$,3) | C. | x∈[1,2] | D. | x∈[1,3) |
2.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
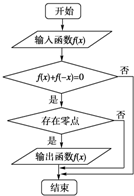

| A. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | B. | f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$$<x<\frac{π}{2}$) | ||
| C. | f(x)=$\frac{|x|}{x}$ | D. | f(x)=x2ln(x2+1) |
9.在等比数列{an}中,a3-2a2=2,且5a4是12a3和2a5的等差中项,则{an}的公比为( )
| A. | 2 | B. | 3 | C. | 2或3 | D. | 6 |
6.“a<1”是“x+$\frac{1}{x+1}$≥a对x∈(-1,+∞)恒成立”的( )
| A. | 充分且不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
3.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的渐近线方程是( )
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{4}{9}$x | C. | y=±$\frac{3}{2}$x | D. | y=±$\frac{9}{4}$x |
 若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则图中的阴影部分的面积为$\frac{2-\sqrt{3}}{2}$.
若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则图中的阴影部分的面积为$\frac{2-\sqrt{3}}{2}$.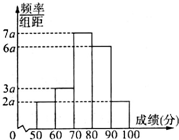 100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则模块测试成绩落在[50,70)中的学生人数是25.
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则模块测试成绩落在[50,70)中的学生人数是25.