题目内容
设a、b、c、d、m、n∈R+,P=
+
,Q=
•
,则有( )
| ab |
| cd |
| ma+nc |
|
分析:先将Q=
•
整理为
,再利用基本不等式来解决.
| ma+nc |
|
ab+cd+ad•
|
解答:解:由于a、b、c、d、m、n∈R+,
则Q=
•
=
=
≥
=
+
=P
当且仅当ad•
=bc•
时,取等号.
故答案为 B
则Q=
| ma+nc |
|
(ma+nc)(
|
=
ab+cd+ad•
|
ab+cd+2
|
| ab |
| cd |
当且仅当ad•
| m |
| n |
| n |
| m |
故答案为 B
点评:本题考查利用基本不等式解决不等式的大小关系,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
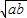 +
+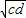 ,Q=
,Q=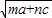 •
•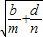 ,则有( )
,则有( )