题目内容
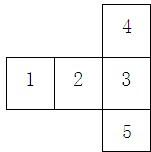 25、编号为A、B、C、D、E的五个小球放在如图所示的五个盒子中,要求每个盒子只能放一个小球,且A不能放1,2号,B必需放在与A相邻的盒子中,则不同的放法有( )种
25、编号为A、B、C、D、E的五个小球放在如图所示的五个盒子中,要求每个盒子只能放一个小球,且A不能放1,2号,B必需放在与A相邻的盒子中,则不同的放法有( )种分析:根据题意,A不能放1,2号,则A可以放在3、4、5号盒子,但“A在3、5号盒子时”与“A在4号盒子时”,B的放法情况数目不同,据此分两种情况讨论,分别求得其情况数目,进而由加法原理,计算可得答案.
解答:解:根据题意,A不能放1,2号,则A可以放在3、4、5号盒子,
分2种情况讨论:
①当A在3、5号盒子时,B有1种放法,剩下3个有A33=6种不同放法,此时,共有2×1×6=12种情况;
②当A在4号盒子时,B有3种放法,剩下3个有A33=6种不同放法,此时,共有1×3×6=18种情况;
由加法原理,计算可得共有12+18=30种不同情况;
故选C.
分2种情况讨论:
①当A在3、5号盒子时,B有1种放法,剩下3个有A33=6种不同放法,此时,共有2×1×6=12种情况;
②当A在4号盒子时,B有3种放法,剩下3个有A33=6种不同放法,此时,共有1×3×6=18种情况;
由加法原理,计算可得共有12+18=30种不同情况;
故选C.
点评:本题考查排列、组合的应用,排列组合问题解法比较固定,关键在于背景材料的创新变化,平时要加强训练.

练习册系列答案
相关题目
 15、编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能放一个小球,且A不能放1,2号,B必须放在与A相邻的盒子中,则不同的放法有
15、编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能放一个小球,且A不能放1,2号,B必须放在与A相邻的盒子中,则不同的放法有 (1)编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能一个小球,且A球不能放在1,2号,B球必须放在与A球相邻的盒子中,不同的放法有多少种?
(1)编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能一个小球,且A球不能放在1,2号,B球必须放在与A球相邻的盒子中,不同的放法有多少种?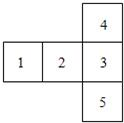 编号为A、B、C、D、E的5种蔬菜种在如右图所示的五块实验田里,每块只能种一种蔬菜,要求A品种不能种在1,2试验田里,B品种必须与A种在相邻的两块田里,则不同的种植方法种数为( )
编号为A、B、C、D、E的5种蔬菜种在如右图所示的五块实验田里,每块只能种一种蔬菜,要求A品种不能种在1,2试验田里,B品种必须与A种在相邻的两块田里,则不同的种植方法种数为( )