题目内容
在边长为6的正△ABC中，点M满足
=2
，则
•
等于（ ）
| BM |
| MA |
| CM |
| CB |
分析：由已知可得，
=
+
=
+
，结合向量的数量积的运算即可求解
| CM |
| CB |
| BM |
| CB |
| 2 |
| 3 |
| BA |
解答：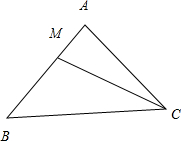
解：∵
=2
，
∴
=
+
=
+
∵＜
，
＞=
，|
|=|
|=6
∴
•
=（
+
）•
=
2+
•
=36+
×6×6×cos120°=24
故选D
解：∵| BM |
| MA |
∴
| CM |
| CB |
| BM |
| CB |
| 2 |
| 3 |
| BA |
∵＜
| BA |
| CB |
| 2π |
| 3 |
| CB |
| BA |
∴
| CM |
| CB |
| CB |
| 2 |
| 3 |
| BA |
| CB |
| CB |
| 2 |
| 3 |
| BA |
| CB |
=36+
| 2 |
| 3 |
故选D
点评：本题主要考查了向量的基本运算及向量的数量积的运算，解题的关键是准确求出向量的夹角．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
（A）（几何证明选讲选做题）如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径作圆与斜边AB交于点D，则BD的长为=
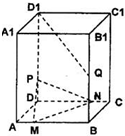已知正四棱柱ABCD-A1B1C1D1的底面边长为4，侧棱长为6，Q为BB1的中点，P∈DD1，M∈AB，N∈CD且AM=1，DN=3，（I）若
．有一动点M在侧面PAB内，它到顶点P的距离与到底面ABC的距离比为
．