题目内容
已知函数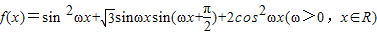 ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为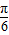 .
.(Ⅰ)求ω的值;
(Ⅱ)若将函数f(x)的图象向右平移
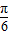 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
【答案】分析:(Ⅰ)用二倍角公式可将函数化简为f(x)=sin(2ωx+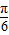 )+
)+ ,再由在y轴右侧的第一个最高点的横坐标为
,再由在y轴右侧的第一个最高点的横坐标为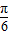 可解得ω=1,
可解得ω=1,
(Ⅱ)由(Ⅰ)得f(x)=sin(2x+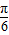 )+
)+ ,由正弦函数的性质,根据图象变换规律得出(x)=sin(
,由正弦函数的性质,根据图象变换规律得出(x)=sin( x-
x-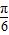 )+
)+ ,令2kπ+
,令2kπ+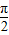 ≤
≤ x-
x-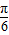 ≤2kπ+
≤2kπ+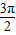 (k∈Z),即可解出其单调增区间.
(k∈Z),即可解出其单调增区间.
解答:解:(Ⅰ)f(x)=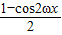 +
+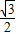 sin2ωx+1+cos2ωx
sin2ωx+1+cos2ωx
=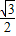 sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=sin(2ωx+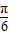 )+
)+ .
.
令2ωx+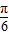 =
=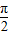 ,将x=
,将x=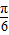 代入可得:ω=1,
代入可得:ω=1,
(Ⅱ)由(Ⅰ)得f(x)=sin(2x+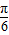 )+
)+ ,
,
函数f(x)的图象向右平移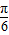 个单位后得出y=sin[2(x-
个单位后得出y=sin[2(x-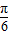 )+
)+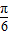 )]+
)]+ =sin(2x-
=sin(2x-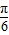 )+
)+ ,
,
再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)=sin( x-
x-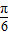 )+
)+ ,
,
最大值为1+ =
= ,
,
令2kπ+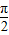 ≤
≤ x-
x-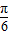 ≤2kπ+
≤2kπ+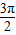 (k∈Z),
(k∈Z),
4kπ+ π≤x≤4kπ+
π≤x≤4kπ+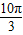 ,
,
单减区间[4kπ+ π,4kπ+
π,4kπ+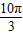 ],(k∈Z).
],(k∈Z).
点评:本题考查了利用两角和与差的公式化简解析式,三角函数的性质,图象变换规律.
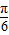 )+
)+ ,再由在y轴右侧的第一个最高点的横坐标为
,再由在y轴右侧的第一个最高点的横坐标为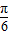 可解得ω=1,
可解得ω=1,(Ⅱ)由(Ⅰ)得f(x)=sin(2x+
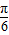 )+
)+ ,由正弦函数的性质,根据图象变换规律得出(x)=sin(
,由正弦函数的性质,根据图象变换规律得出(x)=sin( x-
x-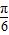 )+
)+ ,令2kπ+
,令2kπ+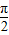 ≤
≤ x-
x-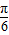 ≤2kπ+
≤2kπ+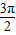 (k∈Z),即可解出其单调增区间.
(k∈Z),即可解出其单调增区间.解答:解:(Ⅰ)f(x)=
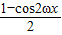 +
+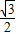 sin2ωx+1+cos2ωx
sin2ωx+1+cos2ωx=
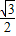 sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=sin(2ωx+
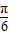 )+
)+ .
.令2ωx+
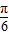 =
=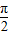 ,将x=
,将x=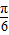 代入可得:ω=1,
代入可得:ω=1,(Ⅱ)由(Ⅰ)得f(x)=sin(2x+
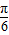 )+
)+ ,
,函数f(x)的图象向右平移
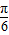 个单位后得出y=sin[2(x-
个单位后得出y=sin[2(x-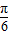 )+
)+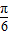 )]+
)]+ =sin(2x-
=sin(2x-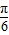 )+
)+ ,
,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)=sin(
 x-
x-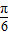 )+
)+ ,
,最大值为1+
 =
= ,
,令2kπ+
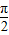 ≤
≤ x-
x-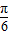 ≤2kπ+
≤2kπ+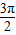 (k∈Z),
(k∈Z),4kπ+
 π≤x≤4kπ+
π≤x≤4kπ+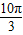 ,
,单减区间[4kπ+
 π,4kπ+
π,4kπ+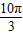 ],(k∈Z).
],(k∈Z).点评:本题考查了利用两角和与差的公式化简解析式,三角函数的性质,图象变换规律.

练习册系列答案
相关题目
 ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为 .
. 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间. ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为 .
. 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间. ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为 .
. 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间. ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为 .
. 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.