题目内容
(07年全国卷Ⅱ)(12分)
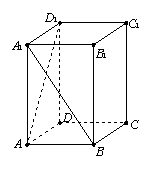
如图,在四棱锥![]() 中,
中,
底面![]() 为正方形,侧棱
为正方形,侧棱![]() 底面
底面![]()
分别为![]() 的中点.
的中点.
(1)证明![]() 平面
平面![]() ;
;
(2)设![]() ,求二面角
,求二面角![]() 的大小.
的大小.

解析:解法一:
(1)作![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点.
的中点.
连结![]() ,又
,又![]() ,
,
故![]() 为平行四边形.
为平行四边形.
![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
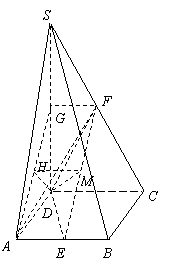
(2)不妨设![]() ,则
,则![]() 为等
为等
腰直角三角形.
取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() ,
,
所以![]() 面
面![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() .
.
连结![]() ,则
,则![]() .
.
故![]() 为二面角
为二面角![]() 的平面角
的平面角
![]() .
.
所以二面角![]() 的大小为
的大小为![]() .
.
解法二:(1)如图,建立空间直角坐标系![]() .
.
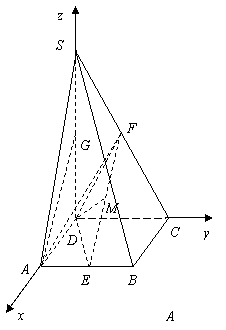
设![]() ,则
,则![]()
![]() ,
,
![]() .
.
取![]() 的中点
的中点![]() ,则
,则![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)不妨设![]() ,则
,则![]() .
.
![]() 中点
中点![]()
又![]() ,
,![]() ,
,
所以向量![]() 和
和![]() 的夹角等于二面角
的夹角等于二面角![]() 的平面角.
的平面角.
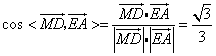 .
.
所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目