题目内容
①存在m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数;
②函数y=
在(-∞,-1)∪(-1,+∞)上是减函数;
③函数=log2x+x2-2在(1,2)内只有一个零点函数;
④定义域内任意两个变量x1,x2,都有
>0,则f(x)在定义域内是增函数
其中正确的结论序号是
②函数y=
| 1 |
| x+1 |
③函数=log2x+x2-2在(1,2)内只有一个零点函数;
④定义域内任意两个变量x1,x2,都有
| f(x1)-f(x2) |
| x1-x2 |
其中正确的结论序号是
①③④
①③④
.分析:对①,根据幂函数的定义判断①是否正确;
对②,根据减函数的定义,举反例验证即可;
对③,利用函数零点的判定定理判断函数的零点存在,再根据单调性判断即可;
对④,根据导数的定义及导数的集合意义,判断④是否正确.
对②,根据减函数的定义,举反例验证即可;
对③,利用函数零点的判定定理判断函数的零点存在,再根据单调性判断即可;
对④,根据导数的定义及导数的集合意义,判断④是否正确.
解答:解:对①,当m=2时,f(x)=x-1 是幂函数,①正确;
对②,取x1=-2<x2=1,y1=-1<y2=
,∴在(-∞,-1)∪(-1,+∞)上不是减函数,②不正确;
对③,∵f(x)的零点是T(x)=x2+x-3的零点,T(1)=-1,T(2)=3,∵T(1)•T(2)<0,∴函数在(1,2)内有零点;
又∵T(x)=x2+x-3在(1,2)单调递增,∴在(1,2)内只有一个零点,∴③正确;
对④,根据定义域内任意两个变量x1,x2,都有
>0,∴f′(x)>0,∴f(x)是增函数,④正确.
答案是①③④
对②,取x1=-2<x2=1,y1=-1<y2=
| 1 |
| 2 |
对③,∵f(x)的零点是T(x)=x2+x-3的零点,T(1)=-1,T(2)=3,∵T(1)•T(2)<0,∴函数在(1,2)内有零点;
又∵T(x)=x2+x-3在(1,2)单调递增,∴在(1,2)内只有一个零点,∴③正确;
对④,根据定义域内任意两个变量x1,x2,都有
| f(x1)-f(x2) |
| x1-x2 |
答案是①③④
点评:本题借助考查命题的真假判断,考查幂函数的定义、函数的单调性、函数的零点判定及导数的定义及几何意义.

练习册系列答案
相关题目
 .
. ,方程
,方程 有2个不等实根,
有2个不等实根, ;
;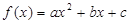 .
. ,方程
,方程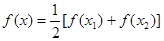 有2个不等实根,
有2个不等实根,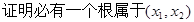 ;
;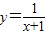 在(-∞,-1)∪(-1,+∞)上是减函数;
在(-∞,-1)∪(-1,+∞)上是减函数;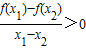 ,则f(x)在定义域内是增函数
,则f(x)在定义域内是增函数