题目内容
已知向量
与
关于x轴对称,j=(0,1),则满足不等式
2+j•
≤0的点Z(x,y)的集合用阴影表示为如图中的( )
| OZ |
| OZ′ |
| OZ |
| ZZ/ |
A、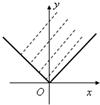 |
B、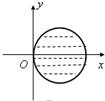 |
C、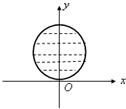 |
D、 |
分析:根据所给的z的坐标,写出题目中要用的向量的坐标,把整理好的坐标都代入条件中所给的不等式,表示出坐标形式的不等式,整理出关于圆的形式,得到图象.
解答:解:向量
与
关于x轴对称,点Z(x,y)
∴
=(x,y),
=(x,-y)
∵j=(0,1),
∴不等式
2+j•
≤0可以整理为x2+y2+-2y≤0
即x2+(y-1)2≤1,
∴对应的图象是以(0,1)为圆心,1为半径的圆及圆内的部分,得到图象,
故选C.
| OZ |
| OZ′ |
∴
| OZ |
| OZ′ |
∵j=(0,1),
∴不等式
| OZ |
| ZZ/ |
即x2+(y-1)2≤1,
∴对应的图象是以(0,1)为圆心,1为半径的圆及圆内的部分,得到图象,
故选C.
点评:本题考查复数与向量的对应,考查关于坐标轴对称的点的坐标,考查向量的数量积,是一个基础题,解题的关键是熟悉复平面上的点,与复数的对应,与向量的对应.

练习册系列答案
相关题目