题目内容

设向量
a
，
b
是非零向量，若函数f（x）=（x
a
+
b
）•（
a
-x
b
）（x∈R）的图象不是直线，且在x=0处取得最值，则必有（　　）
分析：先将函数f（x）进行化简，因为函数的图象不是直线，所以二次项系数不等于0，且在x=0处取得最值，则二次函数的形式为y=ax2+b的形式，从而得到一次项系数为0．
解答：解：因为f（x）=（x
a
+
b
）•（
a
-x
b
）═x
a
2+
a
?
b
-x2
a
?
b
-x
b
2=-(
a
?
b
)x2+(
a
2-
b
2)?x+
a
?
b
，
因为f（x）的图象不是直线，所以-(
a
?
b
)≠0，即
a
?
b
≠0，所以此时
a
，
b
不垂直．
此时函数f（x）为二次函数，因为函数f（x）在x=0处取得最值，则必有
a
2-
b
2=0，即|
a
|=|
b
|，
所以必有时
a
，
b
不垂直且|
a
|=|
b
|．
故选C．
点评：本题主要考查二次函数的图象和性质，以及向量的数量积运算．
练习册系列答案
相关题目
给出下列命题：
（1）设
a
、
b
都是非零向量，则“
a
•
b
=±|
a
|•|
b
|”是“
a
、
b
共线”的充要条件
（2）将函数y=sin（2x+
π
3
）的图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
（3）在△ABC中，若AB=2，AC=3，∠ABC=
π
3
，则△ABC必为锐角三角形；
（4）在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点；
其中正确命题的序号是
（1）（3）
（1）（3）
（写出所有正确命题的序号）．

选择题：

(1)如果a，b是两个单位向量，那么下列四个结论中正确的是

[　　]

(A)a＝b

(B)a·b＝1

(C)

(D)

(2)对于任意向量a、b，下列命题中正确的是

[　　]

(A)若a，b满足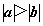，且a与b同向，则a＞b

(B)

(C)

(D)

(3)在四边形ABCD中，若，则

[　　]

(A)ABCD是矩形

(B)ABCD是菱形

(C)ABCD是正方形

(D)ABCD是平行四边形

(4)设a是非零向量，λ是非零实数，下列结论中正确的是

[　　]

(A)a与－λa的方向相反

(B)

(C)a与的方向相同

(D)

(5)设M是□ABCD的对角线的交点，O为任意一点，则等于

[　　]

(A)

(B)2

(C)3

(D)4

(6)下列各组向量中，可以作为基底的是

[　　]

(A)，

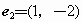
(B)，

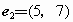
(C)，

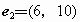
(D)，
给出下列命题：
（1）设
a
、
b
都是非零向量，则“
a
•
b
=±|
a
|•|
b
|”是“
a
、
b
共线”的充要条件
（2）将函数y=sin（2x+
π
3
）的图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
（3）在△ABC中，若AB=2，AC=3，∠ABC=
π
3
，则△ABC必为锐角三角形；
（4）在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点；
其中正确命题的序号是______（写出所有正确命题的序号）．
设a,b都是非零向量，

（1）若向量a与b反向，则a-b与a的方向_________，且|a-b|_________|a|+|b|;

（2）若a与b同向，且|a|＞|b|则a-b与a的方向_________且|a-b|_________|a|-|b|.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网