题目内容
设数列{a}是公差为d的等差数列,其前n项和为Sn.已知a1=1,d=2,(1)求当n∈N*时,
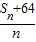 的最小值;
的最小值;(2)当n∈N*时,求证:
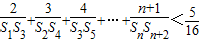 .
.
【答案】分析:(1)利用等差数列的求和公式,求得Sn,进而利用基本不等式,可求 的最小值;
的最小值;
(2)利用裂项法求和,再利用放缩法,可得结论.
解答:(1)解:∵a1=1,d=2,∴
∴ (当且仅当n=8时取等号).
(当且仅当n=8时取等号).
∴ 的最小值为16.…(6分)
的最小值为16.…(6分)
(2)证明:由①知 ,
, =
= =
= …(8分)
…(8分)

= [(
[( )+(
)+( )+…+(
)+…+( )]…(10分)
)]…(10分)
=


即 .…(13分)
.…(13分)
点评:本题考查等差数列的求和公式,考查基本不等式的运用,考查不等式的证明,考查裂项法,属于中档题.
 的最小值;
的最小值;(2)利用裂项法求和,再利用放缩法,可得结论.
解答:(1)解:∵a1=1,d=2,∴

∴
 (当且仅当n=8时取等号).
(当且仅当n=8时取等号).∴
 的最小值为16.…(6分)
的最小值为16.…(6分)(2)证明:由①知
 ,
, =
= =
= …(8分)
…(8分)
=
 [(
[( )+(
)+( )+…+(
)+…+( )]…(10分)
)]…(10分)=



即
 .…(13分)
.…(13分)点评:本题考查等差数列的求和公式,考查基本不等式的运用,考查不等式的证明,考查裂项法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
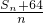 的最小值;
的最小值;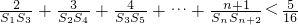 .
.