题目内容
如图,在平面直角坐标系 中,以x轴为始边作两个锐角
中,以x轴为始边作两个锐角 、
、 ,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为
,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为 ;B点的纵坐标为
;B点的纵坐标为 .则
.则 .
.
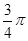
解析试题分析:单位圆的半径是1,根据勾股定理以及点A的横坐标为 ,B点的纵坐标为
,B点的纵坐标为 ,可知点A的纵坐标为
,可知点A的纵坐标为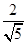 ,点B的横坐标为
,点B的横坐标为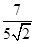 ,所以
,所以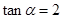 ,
,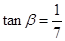 ,
, ,
,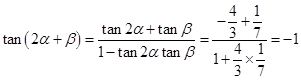 ,因为
,因为 ,
, 是锐角,所以
是锐角,所以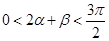 ,所以
,所以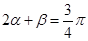 .
.
考点:1.任意角的三角函数;2.三角函数的和角公式

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
题目内容
如图,在平面直角坐标系 中,以x轴为始边作两个锐角
中,以x轴为始边作两个锐角 、
、 ,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为
,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为 ;B点的纵坐标为
;B点的纵坐标为 .则
.则 .
.
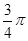
解析试题分析:单位圆的半径是1,根据勾股定理以及点A的横坐标为 ,B点的纵坐标为
,B点的纵坐标为 ,可知点A的纵坐标为
,可知点A的纵坐标为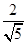 ,点B的横坐标为
,点B的横坐标为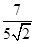 ,所以
,所以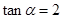 ,
,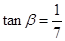 ,
, ,
,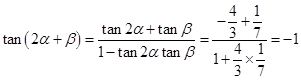 ,因为
,因为 ,
, 是锐角,所以
是锐角,所以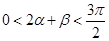 ,所以
,所以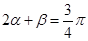 .
.
考点:1.任意角的三角函数;2.三角函数的和角公式

 灵星计算小达人系列答案
灵星计算小达人系列答案