题目内容
已知圆![]() :
:![]() ,抛物线
,抛物线![]() 以圆心
以圆心![]() 为焦点,以坐标原点为顶点.w.w.w.k.s.5.u.c.o.m
为焦点,以坐标原点为顶点.w.w.w.k.s.5.u.c.o.m ![]()
![]()
⑴求抛物线![]() 的方程;
的方程;
⑵设圆![]() 与抛物线
与抛物线![]() 在第一象限的交点为
在第一象限的交点为![]() ,过
,过![]() 作抛物线
作抛物线![]() 的切线与
的切线与![]() 轴的交点为
轴的交点为![]() ,动点
,动点![]() 到
到![]() 、
、![]() 两点距离之和等于
两点距离之和等于![]() ,求
,求![]() 的轨迹方程.
的轨迹方程.
解析:⑴圆![]() 的圆心
的圆心![]() ……1分,设抛物线
……1分,设抛物线![]() :
:![]() ……2分
……2分
![]() ……3分,所以
……3分,所以![]() ,所求抛物线的方程为
,所求抛物线的方程为![]() 或
或![]() ……4分.
……4分.
⑵由方程组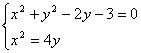 ……5分,依题意解得
……5分,依题意解得![]() ……5分,
……5分,
抛物线![]() 即函数
即函数![]() 的图象,当
的图象,当![]() 时,切线的斜率
时,切线的斜率![]() ……6分,
……6分,
切线为![]() ,即
,即![]() ……7分,
……7分,
![]() 时,
时,![]() ,所以
,所以![]() ……8分.
……8分.
![]() 的轨迹是焦点在
的轨迹是焦点在![]() 轴的椭圆,设它的方程为
轴的椭圆,设它的方程为![]() ……10分,
……10分,
![]() 则
则![]() ,
,![]() ……13分,解得
……13分,解得![]() ,
,![]() ,
,![]() 的轨迹方程为
的轨迹方程为![]() ……12分.
……12分.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知圆的方程为x2+y2=4,若抛物线过点A(-1,0),B(1,0),且以圆的切线为准线,则抛物线的焦点轨迹方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
(本小题满分14分)
已知圆![]() :
:![]() ,抛物线
,抛物线![]() 以圆心
以圆心![]() 为焦点,以坐标原点为顶点.
为焦点,以坐标原点为顶点.
⑴ 求抛物线![]() 的方程;
的方程;
⑵ 设圆![]() 与抛物线
与抛物线![]() 在第一象限的交点为
在第一象限的交点为![]() ,过
,过![]() 作抛物线
作抛物线![]() 的切线与
的切线与![]() 轴的交点为
轴的交点为![]() ,动点
,动点![]() 到
到![]() 、
、![]() 两点距离之和等于
两点距离之和等于![]() ,求
,求![]() 的轨迹方程.
的轨迹方程.
 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为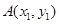 、
、 (其中
(其中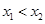 ).
). ,求
,求 与
与 的值;
的值; 与直线
与直线 相切,求圆
相切,求圆 ,且以点
,且以点 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴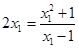 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。 ,借助于函数的性质圆
,借助于函数的性质圆
 可得,
可得, . ------1分
. ------1分 ,
,
 ,或
,或 , --------------------3分
, --------------------3分 ,或
,或 ----------------4分
----------------4分 ,
, ,
, ,则
,则 ,
, ,又
,又 ,
, ,即
,即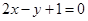 . -----------------7分
. -----------------7分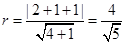 ,--------------8分
,--------------8分 . --------------------9分
. --------------------9分
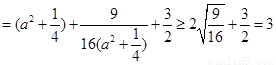 ,
, ,即
,即 ,
, 时取等号.
时取等号.