题目内容
设函数D(x)=
,则下列结论错误的是( )
|
分析:由函数值域的定义易知A错误,D结论正确;由函数单调性定义,易知C结论正确;由偶函数定义可证明B结论正确;即得正确结论.
解答:解:由于函数D(x)=
,则函数值域为{0,1},故D显然正确,A不正确;
∵D(x)=
=D(x),∴D(x)是偶函数,B正确;
∵D(2)=0,D(
)=1,D(1)=0,显然函数D(x)不是单调函数,C正确;
故答案为:A.
|
∵D(x)=
|
∵D(2)=0,D(
| 2 |
故答案为:A.
点评:本题主要考查了函数的定义,偶函数的定义和判断方法,函数周期性的定义和判断方法,函数单调性的意义,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
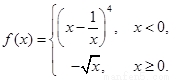 ,
则当x>0时,
,
则当x>0时, 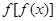 表达式的展开式中常数项为 ( )
表达式的展开式中常数项为 ( )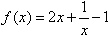 ,(x<0),则f(x)
,(x<0),则f(x)