题目内容
(本小题满分12分)
已知函数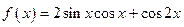 (
(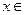 R).
R).
(1) 当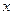 取什么值时,函数
取什么值时,函数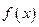 取得最大值,并求其最大值;
取得最大值,并求其最大值;
(2)若 为锐角,且
为锐角,且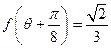 ,求
,求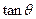 的值.
的值.
已知函数
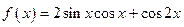 (
(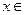 R).
R).(1) 当
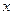 取什么值时,函数
取什么值时,函数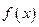 取得最大值,并求其最大值;
取得最大值,并求其最大值;(2)若
 为锐角,且
为锐角,且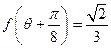 ,求
,求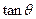 的值.
的值.(本小题主要考查三角函数性质, 同角三角函数的基本关系、两倍角公式等知识, 考查化归与转化的数学思想方法和运算求解能力)
(1) 解: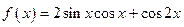
 …… 1分
…… 1分
 …… 2分
…… 2分
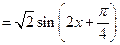 . …… 3分
. …… 3分
∴当 ,即
,即 Z
Z 时,函数
时,函数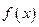 取得最大值,其值为
取得最大值,其值为 .
.
…… 5分
(2)解法1:∵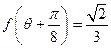 , ∴
, ∴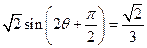 . …… 6分
. …… 6分
∴ . …… 7分
. …… 7分
∵ 为锐角,即
为锐角,即 , ∴
, ∴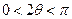 .
.
∴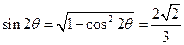 . …… 8分
. …… 8分
∴ . …… 9分
. …… 9分
∴ . …… 10分
. …… 10分
∴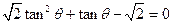 .
.
∴ .
.
∴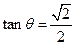 或
或 (不合题意,舍去) …… 11分
(不合题意,舍去) …… 11分
∴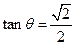 . …… 12分
. …… 12分
解法2: ∵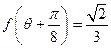 , ∴
, ∴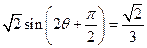 .
.
∴ . …… 7分
. …… 7分
∴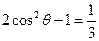 . …… 8分
. …… 8分
∵ 为锐角,即
为锐角,即 ,
,
∴ . …… 9分
. …… 9分
∴ . …… 10分
. …… 10分
∴ . …… 12分
. …… 12分
解法3:∵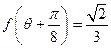 , ∴
, ∴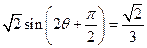 .
.
∴ . …… 7分
. …… 7分
∵ 为锐角,即
为锐角,即 , ∴
, ∴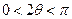 .
.
∴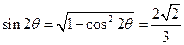 . …… 8分
. …… 8分
∴ …… 9分
…… 9分
 …… 10分
…… 10分

 . …… 12分
. …… 12分
(1) 解:
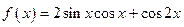
 …… 1分
…… 1分 …… 2分
…… 2分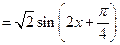 . …… 3分
. …… 3分∴当
 ,即
,即 Z
Z 时,函数
时,函数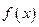 取得最大值,其值为
取得最大值,其值为 .
.…… 5分
(2)解法1:∵
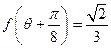 , ∴
, ∴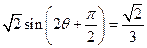 . …… 6分
. …… 6分∴
 . …… 7分
. …… 7分∵
 为锐角,即
为锐角,即 , ∴
, ∴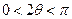 .
.∴
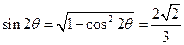 . …… 8分
. …… 8分∴
 . …… 9分
. …… 9分∴
 . …… 10分
. …… 10分∴
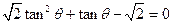 .
.∴
 .
.∴
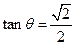 或
或 (不合题意,舍去) …… 11分
(不合题意,舍去) …… 11分∴
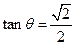 . …… 12分
. …… 12分解法2: ∵
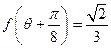 , ∴
, ∴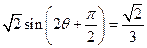 .
.∴
 . …… 7分
. …… 7分∴
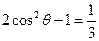 . …… 8分
. …… 8分∵
 为锐角,即
为锐角,即 ,
,∴
 . …… 9分
. …… 9分∴
 . …… 10分
. …… 10分∴
 . …… 12分
. …… 12分解法3:∵
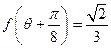 , ∴
, ∴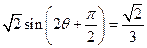 .
.∴
 . …… 7分
. …… 7分∵
 为锐角,即
为锐角,即 , ∴
, ∴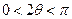 .
.∴
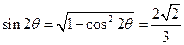 . …… 8分
. …… 8分∴
 …… 9分
…… 9分 …… 10分
…… 10分
 . …… 12分
. …… 12分略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,
, ,
, ,
, ,
, ;
;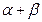 .
. 则
则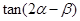 的值是 ( )
的值是 ( )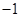
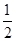

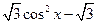 的图象相邻的两条对称之间的距离是___
的图象相邻的两条对称之间的距离是___ .
. 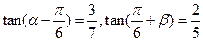 ,则
,则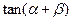 的值为
的值为

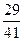
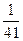

 的值为
的值为





 ,则
,则
 ( )
( )


