题目内容
已知 ,
,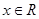 ,函数
,函数 ;
;
(I)求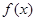 的最小正周期;
的最小正周期;
(II)求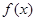 在区间
在区间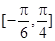 上的最大值和最小值。
上的最大值和最小值。
【答案】
(I)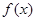 的最小正周期为
的最小正周期为 ;
;
(II) 时,函数
时,函数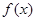 取得最大值2;
取得最大值2; 时,函数
时,函数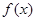 取得最小值
取得最小值 ;
;
【解析】
试题分析:(法一)(I)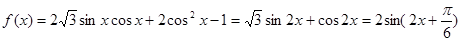 ,
,
函数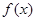 的最小正周期为
的最小正周期为 ;
4分
;
4分
(II)因为 ,
5分
,
5分
所以,当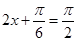 即
即 时,函数
时,函数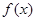 取得最大值2;
取得最大值2;
当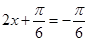 即
即 时,函数
时,函数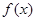 取得最小值
取得最小值 ;
9分
;
9分
(法二)(I) ,
,
函数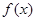 的最小正周期为
的最小正周期为 ;
4分
;
4分
(II)因为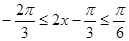 ,
5分
,
5分
所以,当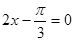 即
即 时,函数
时,函数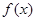 取得最大值2;
取得最大值2;
当 即
即 时,函数
时,函数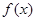 取得最小值
取得最小值 ;
9分
;
9分
考点:本题主要考查平面向量的数量积,三角函数中两角和的正、余弦公式、二倍角公式;三角函数的周期、单调、最值等性质;考查三角函数与平面向量的综合运用能力和化归与转化思想。
点评:典型题,为研究三角函数的图象和性质,往往需要将函数“化一”,这是常考题型。本题首先通过平面向量的坐标运算,计算向量的数量积得到函数F(x)的表达式,并运用“三角公式”进行化简,为进一步解题奠定了基础。

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 ,
, ,函数
,函数 ;
; 时,求f(x)的取值范围.
时,求f(x)的取值范围. ,
, ,函数
,函数 ;
; 时,求f(x)的取值范围.
时,求f(x)的取值范围.