题目内容
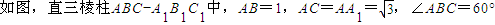
(1)证明:AB⊥A1C
(2)求二面角A1-BC-A的余弦值.
【答案】分析:(1)根据AB=1,AC=AA1= ,∠ABC=60°,可知AB⊥AC,而A1A⊥平面ABC,AB?平面ABC,根据线面垂直的性质可知AB⊥A1A,又AC∩A1A=A,根据线面垂直的判定定理可知AB⊥平面A1ACC1,又A1C?平面A1ACC1,从而AB⊥A1C;
,∠ABC=60°,可知AB⊥AC,而A1A⊥平面ABC,AB?平面ABC,根据线面垂直的性质可知AB⊥A1A,又AC∩A1A=A,根据线面垂直的判定定理可知AB⊥平面A1ACC1,又A1C?平面A1ACC1,从而AB⊥A1C;
(2)以A为坐标原点,AB,AC,AA1,分别为x,y,z轴正方向建立空间坐标,分别求出平面ABC的一个法向量和平面A1BC的一个法向量,代入向量夹角公式,可得答案.
解答: 证明:(I)∵AB=1,AC=AA1=
证明:(I)∵AB=1,AC=AA1= ,∠ABC=60°
,∠ABC=60°
∴AB⊥AC
∵直三棱柱ABC-A1B1C1中
∴A1A⊥平面ABC,而AB?平面ABC
∴AB⊥A1A,又AC∩A1A=A
∴AB⊥平面A1ACC1,而A1C?平面A1ACC1,
∴AB⊥A1C;
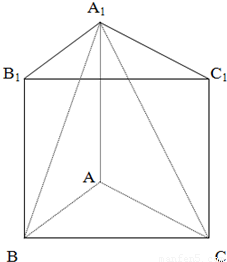
解:(II)建立如图所示的空间坐标系
由AB=1,AC=AA1= ,得
,得
则A(0,0,0),B(1,0,0),C(0, ,0),A1(0,0,
,0),A1(0,0, )
)
由A1A⊥平面ABC,可得 =(0,0,
=(0,0, )是平面ABC的一个法向量
)是平面ABC的一个法向量
设 =(x,y,z)是平面A1BC的一个法向量,由
=(x,y,z)是平面A1BC的一个法向量,由 =(-1,
=(-1, ,0),
,0), =(1,0,-
=(1,0,- )
)
可得 ,即
,即
令x= ,则
,则 =(
=( ,1,1)
,1,1)
设二面角A1-BC-A的平面角为θ
则cosθ= =
= =
=
点评:本题考查的知识点是二面角的求法,线面垂直的判定与性质,(1)的关键是熟练掌握空间线面垂直与线线垂直的相互转化,(2)的关键是建立坐标系,将二面角转化为向量夹角.
 ,∠ABC=60°,可知AB⊥AC,而A1A⊥平面ABC,AB?平面ABC,根据线面垂直的性质可知AB⊥A1A,又AC∩A1A=A,根据线面垂直的判定定理可知AB⊥平面A1ACC1,又A1C?平面A1ACC1,从而AB⊥A1C;
,∠ABC=60°,可知AB⊥AC,而A1A⊥平面ABC,AB?平面ABC,根据线面垂直的性质可知AB⊥A1A,又AC∩A1A=A,根据线面垂直的判定定理可知AB⊥平面A1ACC1,又A1C?平面A1ACC1,从而AB⊥A1C;(2)以A为坐标原点,AB,AC,AA1,分别为x,y,z轴正方向建立空间坐标,分别求出平面ABC的一个法向量和平面A1BC的一个法向量,代入向量夹角公式,可得答案.
解答:
 证明:(I)∵AB=1,AC=AA1=
证明:(I)∵AB=1,AC=AA1= ,∠ABC=60°
,∠ABC=60°∴AB⊥AC
∵直三棱柱ABC-A1B1C1中
∴A1A⊥平面ABC,而AB?平面ABC
∴AB⊥A1A,又AC∩A1A=A
∴AB⊥平面A1ACC1,而A1C?平面A1ACC1,
∴AB⊥A1C;
解:(II)建立如图所示的空间坐标系
由AB=1,AC=AA1=
 ,得
,得则A(0,0,0),B(1,0,0),C(0,
 ,0),A1(0,0,
,0),A1(0,0, )
)由A1A⊥平面ABC,可得
 =(0,0,
=(0,0, )是平面ABC的一个法向量
)是平面ABC的一个法向量设
 =(x,y,z)是平面A1BC的一个法向量,由
=(x,y,z)是平面A1BC的一个法向量,由 =(-1,
=(-1, ,0),
,0), =(1,0,-
=(1,0,- )
)可得
 ,即
,即
令x=
 ,则
,则 =(
=( ,1,1)
,1,1)设二面角A1-BC-A的平面角为θ
则cosθ=
 =
= =
=
点评:本题考查的知识点是二面角的求法,线面垂直的判定与性质,(1)的关键是熟练掌握空间线面垂直与线线垂直的相互转化,(2)的关键是建立坐标系,将二面角转化为向量夹角.

练习册系列答案
相关题目
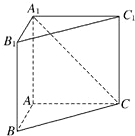 如图所示,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图所示,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1= 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=