题目内容
海水受日月的引力作用,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是港口在某季节每天的时间与水深关系的表格:
选用函数y=Asin(ωx+φ)+B(A>0,ω>0)来模拟港口的水深与时间的关系.如果一条货船的吃水深度是5米,安全条例规定至少有1.25米的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
8
8
小时.分析:根据函数的周期算出ω=
,由振幅的大小和平衡位置的水深得出A=2.5,B=5.再由x=3时y=7.5,达到最大值,
建立关系式解出φ=2kπ(k∈Z)从而得到函数的表达式为:y=2.5sin
x+5(0≤x≤24).最后根据安全间隙的规定解关于x的不等式,结合0≤x≤24,得1≤x≤5或13≤x≤17,即可算出该船一天之内在港口内呆的时间总和.
| π |
| 6 |
建立关系式解出φ=2kπ(k∈Z)从而得到函数的表达式为:y=2.5sin
| π |
| 6 |
解答:解:由题意知,可得
∵函数y=f(x)的周期T=12,振幅A=2.5,B=5,∴ω=
=
,
又∵x=3时y=7.5,达到最大值,
∴由7.5=2.5sin(
×3+φ)+5,得sin(
+φ)=1,
即cosφ=1,得φ=2kπ(k∈Z).
∴函数的表达式为:y=2.5sin
x+5(0≤x≤24);
由该船进出港时,水深应不小于5+1.25=6.25(m),
∴当y≥6.25时,货船就可以进港,即2.5sin
x+5≥6.25,
∴sin
x≥
,得
+2kπ≤
x≤
+2kπ(k∈Z)
即1+12k≤x≤5+12k(k∈Z),结合0≤x≤24,得1≤x≤5或13≤x≤17.
即该船一天之内在港口内呆的时间段为凌晨1点到5点和下午13点到17点,停留的总时间为8小时
故答案为:8
∵函数y=f(x)的周期T=12,振幅A=2.5,B=5,∴ω=
| 2π |
| 12 |
| π |
| 6 |
又∵x=3时y=7.5,达到最大值,
∴由7.5=2.5sin(
| π |
| 6 |
| π |
| 2 |
即cosφ=1,得φ=2kπ(k∈Z).
∴函数的表达式为:y=2.5sin
| π |
| 6 |
由该船进出港时,水深应不小于5+1.25=6.25(m),
∴当y≥6.25时,货船就可以进港,即2.5sin
| π |
| 6 |
∴sin
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
即1+12k≤x≤5+12k(k∈Z),结合0≤x≤24,得1≤x≤5或13≤x≤17.
即该船一天之内在港口内呆的时间段为凌晨1点到5点和下午13点到17点,停留的总时间为8小时
故答案为:8
点评:本题给出实际应用问题,求轮船在港口停留的总时长.着重考查了三角函数解析式求法和运用三角函数模型的解决应用问题等知识,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
海水受日月的引力作用,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是港口在某季节每天的时间与水深关系的表格:
|
时刻 |
0:00 |
3:00 |
6:00 |
9:00 |
12:00 |
15:00 |
18:00 |
21:00 |
24:00 |
|
水深 |
5.0 |
7.5 |
5.0 |
2.5 |
5.0 |
7.5 |
5.0 |
2.5 |
5.0 |
选用函数 来模拟港口的水深与时间的关系.如果一条货船的吃水深度是4米,安全条例规定至少有
来模拟港口的水深与时间的关系.如果一条货船的吃水深度是4米,安全条例规定至少有 米的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为____________小时
米的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为____________小时
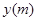 是时间
是时间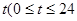 ,单位:
,单位: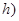 的函数,记作:
的函数,记作: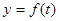 ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
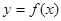 的曲线可以近似地看做函数
的曲线可以近似地看做函数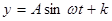 的图象.
的图象.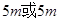 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为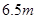 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?