题目内容
已知圆O1,O2,O3为球O的三个小圆,其半径分别为1,1,
,若三个小圆所在的平面两两垂直且公共点P在球面上,则球的表面积为
| 2 |
8π
8π
.分析:由题意可得:三个圆的直径关系为:22+22=(2
)2,因为三个小圆所在的平面两两垂直且公共点P在球面上,所以O3过O1,O2的圆心,即O3是球的大圆,进而结合球的表面积公式可得答案.
| 2 |
解答:解:因为圆O1,O2,O3半径分别为1,1,
,
所以其直径分别为:2,2,2
,并且22+22=(2
)2,
又因为三个小圆所在的平面两两垂直且公共点P在球面上,
所以O3过O1,O2的圆心,
所以O3是球的大圆,即球的半径为
,
所以球的表面积为:S=4πr2=8π.
故答案为:8π.
| 2 |
所以其直径分别为:2,2,2
| 2 |
| 2 |
又因为三个小圆所在的平面两两垂直且公共点P在球面上,
所以O3过O1,O2的圆心,
所以O3是球的大圆,即球的半径为
| 2 |
所以球的表面积为:S=4πr2=8π.
故答案为:8π.
点评:本题主要考查球的有关性质,以及球的表面积公式,考查学生的空间想象能力与逻辑推理论证能力,此题属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
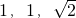 ,若三个小圆所在的平面两两垂直且公共点P在球面上,则球的表面积为________.
,若三个小圆所在的平面两两垂直且公共点P在球面上,则球的表面积为________.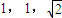 ,若三个小圆所在的平面两两垂直且公共点P在球面上,则球的表面积为 .
,若三个小圆所在的平面两两垂直且公共点P在球面上,则球的表面积为 .