题目内容
已知向量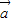 ,
,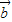 满足
满足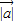 =3,
=3,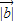 =2,a与b的夹角为60°,则a•b= .若(a-mb)⊥a,则实数m= .
=2,a与b的夹角为60°,则a•b= .若(a-mb)⊥a,则实数m= .
【答案】分析:(1)直接代入向量数量积公式易求答案.
(2)根据向量垂直的充要条件构造方程,解方程即可求出未知参数m的值.
解答:解:(1)∵|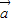 |=3,|
|=3,|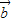 |=2,
|=2,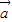 与
与 的夹角为60°
的夹角为60°
∴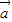 •
•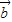 =3×2×
=3×2× =3
=3
又∵(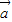 -m
-m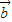 )⊥
)⊥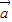
∴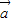 2-m
2-m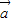 •
•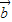 =0
=0
即9-3m=0
解m=3
故答案为:3,3
点评:本题考查的知识点为平面向量的数量积运算,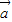 ⊥
⊥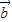 ?x1•x2+y1y2=0.即:“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0.
?x1•x2+y1y2=0.即:“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0.
(2)根据向量垂直的充要条件构造方程,解方程即可求出未知参数m的值.
解答:解:(1)∵|
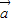 |=3,|
|=3,|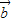 |=2,
|=2,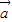 与
与 的夹角为60°
的夹角为60°∴
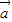 •
•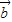 =3×2×
=3×2× =3
=3又∵(
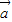 -m
-m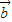 )⊥
)⊥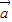
∴
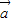 2-m
2-m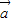 •
•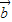 =0
=0即9-3m=0
解m=3
故答案为:3,3
点评:本题考查的知识点为平面向量的数量积运算,
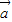 ⊥
⊥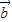 ?x1•x2+y1y2=0.即:“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0.
?x1•x2+y1y2=0.即:“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
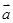 ,
,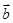 满足|
满足|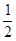 x3+
x3+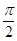 ) B. [0,
) B. [0, 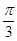 ] C.(
] C.(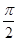 ] D.(
] D.(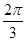 ]
]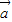 、
、 满足|
满足|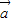 |=3,|
|=3,|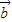 |=2,
|=2,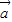 与
与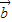 的夹角为60°,则|
的夹角为60°,则|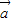 -
-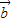 |= .
|= .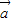 ,
,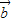 满足
满足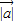 =3,
=3,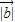 =2,a与b的夹角为60°,则a•b= .若(a-mb)⊥a,则实数m= .
=2,a与b的夹角为60°,则a•b= .若(a-mb)⊥a,则实数m= .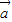 ,
,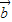 满足|
满足|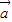 |=3|
|=3|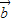 |≠0,且关于x的函数f(x)=
|≠0,且关于x的函数f(x)= x3+
x3+ |
| |x2+
|x2+ •
•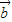 x在R上单调递增,则
x在R上单调递增,则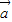 ,
,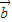 的夹角的取值范围是( )
的夹角的取值范围是( )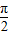 )
) ]
]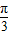 ,
,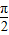 ]
]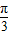 ,
,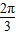 ]
]