题目内容
如果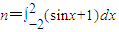
，则（1+2x）（1-x）n的展开式中x2项的系数为（ ）A．2
B．-2
C．-6
D．-8
【答案】分析：由定积分的计算，可得n的值，进而分析在（1+2x）（1-x）n展开式中产生x2项的情况，分2种情况讨论，计算可得答案．
解答：解：根据题意，n=∫-22（sinx+1）dx=2-cos2-（-2）+cos（-2）=4，
则（1+2x）（1-x）4中，x2项产生有2种情况，
①（1+2x）中出常数项，（1-x）4中出x2项，
②（1+2x）与（1-x）4中，都出x项；
则其展开式中x2的系数为1×C42（-1）2+2×C43（-1）=-2；
故选B．
点评：本题考查二项式定理的运用，解题时关键在于对（1+2x）（1-x）n展开式中如何产生x2项的几种情况的分析讨论．
解答：解：根据题意，n=∫-22（sinx+1）dx=2-cos2-（-2）+cos（-2）=4，
则（1+2x）（1-x）4中，x2项产生有2种情况，
①（1+2x）中出常数项，（1-x）4中出x2项，
②（1+2x）与（1-x）4中，都出x项；
则其展开式中x2的系数为1×C42（-1）2+2×C43（-1）=-2；
故选B．
点评：本题考查二项式定理的运用，解题时关键在于对（1+2x）（1-x）n展开式中如何产生x2项的几种情况的分析讨论．
练习册系列答案
相关题目
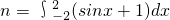，则（1+2x）（1-x）n的展开式中x2项的系数为