题目内容
如图，已知⊙O1和⊙O2相交于A、B两点，C是⊙O1上一点，连结CA、CB交⊙O2于点D、F，过点C作⊙O1的切线CE.猜测CE与DF位置上有何关系？若把两圆相交改为两圆相切，此时又会出现什么结论？若把DF平移到与⊙O1相切于G点，连结AG，则图中会有哪些结论成立？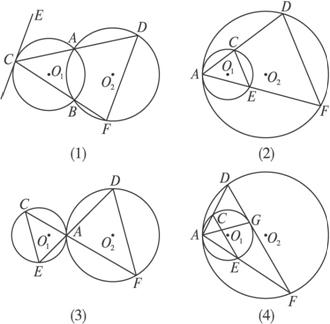
思路解析：观察图形，易猜测CE∥DF，再由弦切角可证明猜测.
解：观察图形，都猜测CE∥DF.
在图(1)中，连结AB，由切线CE，可得∠ACE=∠ABC；又由圆内接四边形ABFD，可得∠ABC=∠ADF.所以，∠ACE=∠ADF，得到CE∥DF.
在图(2)与图(3)中，过点A作两圆的公切线AT，由弦切角易得∠ACE=∠ADF，则CE∥DF.
在图(4)中，过点A作两圆的公切线AT，由弦切角易得∠ACE=∠ADF，则CE∥DF.
练习册系列答案
相关题目
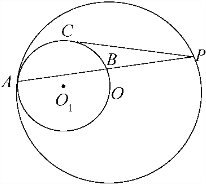如图，已知⊙O和⊙O1内切于点A，⊙O的弦AP交⊙O1于点B，PC切⊙O1于点C，且
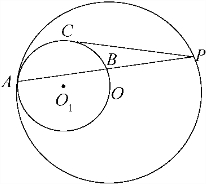如图，已知⊙O和⊙O1内切于点A，⊙O的弦AP交⊙O1于点B，PC切⊙O1于点C，且
=
，则⊙O1和⊙O的半径的比值为多少？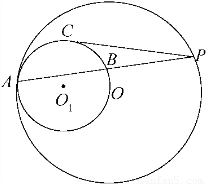
如图，已知⊙O和⊙O1内切于点A，⊙O的弦AP交⊙O1于点B，PC切⊙O1于点C，且
=
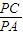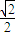，则⊙O1和⊙O的半径的比值为多少？
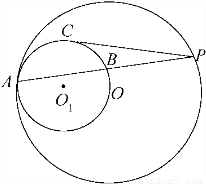如图，已知⊙O和⊙O1内切于点A，⊙O的弦AP交⊙O1于点B，PC切⊙O1于点C，且
=
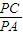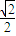，则⊙O1和⊙O的半径的比值为多少？