题目内容
直线y=x-3与抛物线y2=4x交于A、B两点，过A、B两点向抛物线的准线作垂线，垂足分别为P、Q，则梯形APQB的面积为
- A.48
- B.56
- C.64
- D.72
A
分析：依题意联立方程组消去y，进而求得交点的坐标，进而根据|AP|，|BQ|和|PQ|的值求得梯形APQB的面积
解答：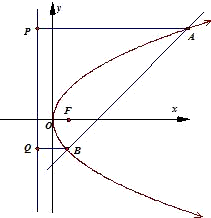
解：直线y=x-3与抛物线y2=4x交于A，B两点，过A，B两点向抛物线的准线作垂线，垂足分别为P，Q，
联立方程组得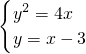
，
消元得x2-10x+9=0，
解得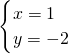
，和
，
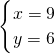∴|AP|=10，|BQ|=2，|PQ|=8，梯形APQB的面积为48，
故选A．
点评：本题主要考查了抛物线与直线的关系．常需要把直线与抛物线方程联立根据韦达定理找到解决问题的途径．
分析：依题意联立方程组消去y，进而求得交点的坐标，进而根据|AP|，|BQ|和|PQ|的值求得梯形APQB的面积
解答：
解：直线y=x-3与抛物线y2=4x交于A，B两点，过A，B两点向抛物线的准线作垂线，垂足分别为P，Q，联立方程组得
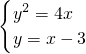，消元得x2-10x+9=0，
解得
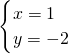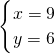，和，∴|AP|=10，|BQ|=2，|PQ|=8，梯形APQB的面积为48，
故选A．
点评：本题主要考查了抛物线与直线的关系．常需要把直线与抛物线方程联立根据韦达定理找到解决问题的途径．
练习册系列答案
阅读快车系列答案
相关题目
，4Bn-12An=13n.
.
），试列出P（x，y）所满足的条件，并求出相应的最大值．
上,且Pn的横坐标构成以
为首项,-1为公差的等差数列{xn}.
+
+…+
＜
;