题目内容
根据抛物线的光学原理:一水平光线射到抛物线上一点,经抛物线反射后,反射光线必过焦点.然后求解此题:抛物线y2=4x上有两个定点A、B分别在对称轴的上、下两侧,一水平光线射到A点后,反射光线会平行y轴,一水平光线射到B点后,反射光线所在直线的斜率为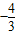 .
.(Ⅰ)求直线AB的方程.
(Ⅱ)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
【答案】分析:(1)由已知得焦点F(1,0),且FA⊥x轴,所以A (1,2),同理得到B(4,-4),由此能求出直线AB的方程.
(2)法一:设在抛物线AOB这段曲线上任一点P(x,y),且1≤x≤4,-4≤y≤2.由点P到直线AB的距离d=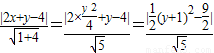 ,由此得到△PAB的面积最大值和此时P点坐标.
,由此得到△PAB的面积最大值和此时P点坐标.
法二: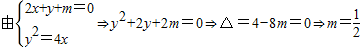 ,由此得到△PAB的面积最大值和此时P点坐标.
,由此得到△PAB的面积最大值和此时P点坐标.
解答:解:(1)由已知得焦点F(1,0),
且FA⊥x轴,
∴A (1,2),
同理 ,
,
得到B(4,-4),
所以直线AB的方程为2x+y-4=0.(6分)
(2)法一:设在抛物线AOB这段曲线上任一点P(x,y),
且1≤x≤4,-4≤y≤2.
则点P到直线AB的距离d=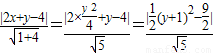 ,
,
所以当y=-1时,d取最大值 ,
,
又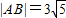 (10分)
(10分)
所以△PAB的面积最大值为 ,
,
此时P点坐标为 .(12分)
.(12分)
法二: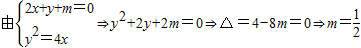 ,
,
∴ ,
,
∴△PAB的面积最大值为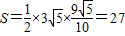 ,
,
此时P点坐标为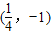 .
.
点评:本题考查直线方程的求法和求△PAB的最大面积.综合性强,难度大,容易出错.解题时要认真审题,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.
(2)法一:设在抛物线AOB这段曲线上任一点P(x,y),且1≤x≤4,-4≤y≤2.由点P到直线AB的距离d=
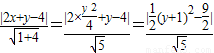 ,由此得到△PAB的面积最大值和此时P点坐标.
,由此得到△PAB的面积最大值和此时P点坐标.法二:
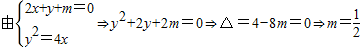 ,由此得到△PAB的面积最大值和此时P点坐标.
,由此得到△PAB的面积最大值和此时P点坐标.解答:解:(1)由已知得焦点F(1,0),
且FA⊥x轴,
∴A (1,2),
同理
 ,
,得到B(4,-4),
所以直线AB的方程为2x+y-4=0.(6分)
(2)法一:设在抛物线AOB这段曲线上任一点P(x,y),
且1≤x≤4,-4≤y≤2.
则点P到直线AB的距离d=
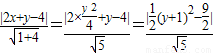 ,
,所以当y=-1时,d取最大值
 ,
,又
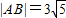 (10分)
(10分)所以△PAB的面积最大值为
 ,
,此时P点坐标为
 .(12分)
.(12分)法二:
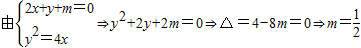 ,
,∴
 ,
,∴△PAB的面积最大值为
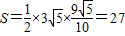 ,
,此时P点坐标为
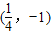 .
.点评:本题考查直线方程的求法和求△PAB的最大面积.综合性强,难度大,容易出错.解题时要认真审题,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.

练习册系列答案
相关题目
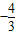 .
.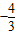 .
.