题目内容
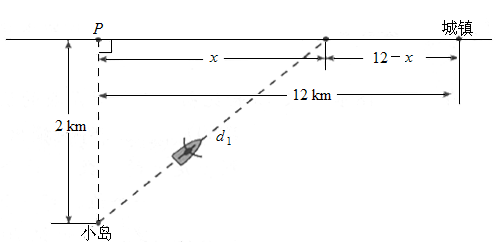
如图，一座小岛距离海岸线上最近的点P的距离是2km，从点P沿海岸正东12km处有一个小镇．（1）假设一个人驾驶的小船的平均速度为3km/h，步行的速度是5km/h，t（单位：h）表示他从小岛到城镇的时间，x（单位：km）表示此人将船停在海岸处距P点的距离．请将t表示为x的函数，并写出定义域．
（2）如果将船停在距点P 4km处，那么从小岛到城镇要多长时间（精确到0.1h）？（
| 5 |
分析：（1）根据总的时间t为驾船行驶的时间与步行到城镇的时间之和，分别表示出从小岛到Q点的时间为
，从Q点到城镇所需的时间为
，即可求得函数t（x），根据实际意义，求得定义域，从而得到答案；
（2）根据题意可知x=4，将x=4代入到t（x）中，求解即可得到从小岛到城镇要多长时间．
| ||
| 3 |
| 12-x |
| 5 |
（2）根据题意可知x=4，将x=4代入到t（x）中，求解即可得到从小岛到城镇要多长时间．
解答：解：（1）总的时间t为驾船行驶的时间与步行到城镇的时间之和，
小岛到Q点的距离：
，
∴从小岛到Q点的时间为：
，
Q点到城镇的距离：12-x，
∴从Q点到城镇所需的时间为：
，
∴t（x）=
+
，0≤x≤12；
（2）∵t（x）=
+
，0≤x≤12，
∴将x=4代入函数t（x），得t（4）=
+
≈3.1（h），
∴从小岛到城镇要3.1h．
小岛到Q点的距离：
| x2+4 |
∴从小岛到Q点的时间为：
| ||
| 3 |
Q点到城镇的距离：12-x，
∴从Q点到城镇所需的时间为：
| 12-x |
| 5 |
∴t（x）=
| ||
| 3 |
| 12-x |
| 5 |
（2）∵t（x）=
| ||
| 3 |
| 12-x |
| 5 |
∴将x=4代入函数t（x），得t（4）=
2
| ||
| 3 |
| 8 |
| 5 |
∴从小岛到城镇要3.1h．
点评：本题主要考查函数模型的选择与应用．解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．属于基础题．
练习册系列答案
相关题目
