题目内容
已知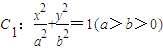 的离心率为
的离心率为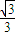 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点F2,直线l1过点F1且垂直于椭圆的长轴,曲线C2上任意一点M到l1距离与MF2相等,求曲线C2的方程.
(3)若A(x1,2),C(x,y),是C2上不同的点,且AB⊥BC,求y的取值范围.
【答案】分析:(1)根据离心率求得a和c的关系,进而根据直线l与圆相切根据圆心到直线的距离为半径求得b,进而求得a,则椭圆方程可得.
(2))根据|MP|=|MF2|可知动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离,进而根据抛物线的定义可知动点M的轨迹是以l1为准线,F2为焦点的抛物线,根据定点直线l1的距离求得抛物线方程中的p,则抛物线方程可得.
(3)由(1)可求得A点坐标,设出B点和C点坐标,表示出 和
和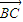 根据AB⊥BC可知
根据AB⊥BC可知 •
•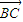 =0,整理得关于y2的一元二次方程根据判别式大于等于0求得y的范围.
=0,整理得关于y2的一元二次方程根据判别式大于等于0求得y的范围.
解答:解:(1)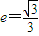 ,
,
∴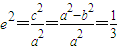 ,
,
∴2a2=3b2
∵直线l:x-y+2=0与圆x2+y2=b2相切,
∴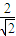 =b,
=b,
∴b=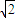 ,b2=2,
,b2=2,
∴a2=3.
∴椭圆C1的方程是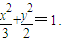
(2)∵|MP|=|MF2|,
∴动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离
∴动点M的轨迹是以l1为准线,F2为焦点的抛物线,
∴ ,p=2,
,p=2,
∴点M的轨迹C2的方程为y2=4x.
(3)由(1)知A(1,2),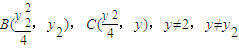 ,y2≠2,①则
,y2≠2,①则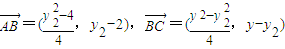 ,
,
又因为 ,
, ,
,
整理得y22+(y+2)y2+16+2y=0,则此方程有解,
∴△=(y+2)2-4•(16+2y)≥0解得y≤-6或y≥10,又检验条件①:
∵y2=2时y=-6,不符合题意.
∴点C的纵坐标y的取值范围是(-∞,-6)∪[10,+∞).
点评:本题主要考查了直线与圆锥曲线的综合问题.涉及了圆锥曲线方程,方程的根,与圆锥曲线性质有关的量的取值范围等问题,是近几年高考的趋向.
(2))根据|MP|=|MF2|可知动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离,进而根据抛物线的定义可知动点M的轨迹是以l1为准线,F2为焦点的抛物线,根据定点直线l1的距离求得抛物线方程中的p,则抛物线方程可得.
(3)由(1)可求得A点坐标,设出B点和C点坐标,表示出
 和
和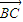 根据AB⊥BC可知
根据AB⊥BC可知 •
•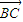 =0,整理得关于y2的一元二次方程根据判别式大于等于0求得y的范围.
=0,整理得关于y2的一元二次方程根据判别式大于等于0求得y的范围.解答:解:(1)
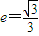 ,
,∴
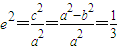 ,
,∴2a2=3b2
∵直线l:x-y+2=0与圆x2+y2=b2相切,
∴
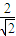 =b,
=b,∴b=
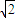 ,b2=2,
,b2=2,∴a2=3.
∴椭圆C1的方程是
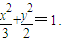
(2)∵|MP|=|MF2|,
∴动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离
∴动点M的轨迹是以l1为准线,F2为焦点的抛物线,
∴
 ,p=2,
,p=2,∴点M的轨迹C2的方程为y2=4x.
(3)由(1)知A(1,2),
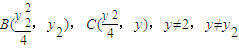 ,y2≠2,①则
,y2≠2,①则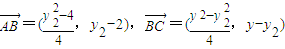 ,
,又因为
 ,
, ,
,整理得y22+(y+2)y2+16+2y=0,则此方程有解,
∴△=(y+2)2-4•(16+2y)≥0解得y≤-6或y≥10,又检验条件①:
∵y2=2时y=-6,不符合题意.
∴点C的纵坐标y的取值范围是(-∞,-6)∪[10,+∞).
点评:本题主要考查了直线与圆锥曲线的综合问题.涉及了圆锥曲线方程,方程的根,与圆锥曲线性质有关的量的取值范围等问题,是近几年高考的趋向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
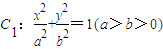 的离心率为
的离心率为 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.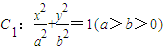 的离心率为
的离心率为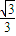 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.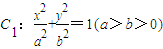 的离心率为
的离心率为 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.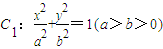 的离心率为
的离心率为 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.