题目内容
椭圆
+
=1中,F1、F2为左、右焦点,A为短轴一端点,弦AB过左焦点F1,则△ABF2的面积为( )
| x2 |
| 6 |
| y2 |
| 3 |
分析:先判断△AOF1是等腰直角三角形,△AOF2也是等腰直角三角形,从而△F1AF2也是等腰直角三角形,故可得∠BAF2=90°,设|BF1|=x,根据椭圆定义,x+|BF2|=2a=2
,利用勾股定理,AB2+AF22=BF22,可求得x=
,从而可求△ABF2的面积.
| 6 |
| ||
| 3 |
解答:解:由题意,a=
,b=
,c=
,|OA|=|OF1|=
,
∴△AOF1是等腰直角三角形,同理△AOF2也是等腰直角三角形,
∴△F1AF2也是等腰直角三角形,
∴|F1A|=|F2A|=
,
∴∠BAF2=90°,
设|BF1|=x,根据椭圆定义,x+|BF2|=2a=2
.
根据勾股定理,AB2+AF22=BF22,
(
+x)2+(
)2=(2
-x)2,
∴x=
,
∴S△ABF2=
|AB|×|AF2|=
(
+
)×
=4.
故选D.
| 6 |
| 3 |
| 3 |
| 3 |
∴△AOF1是等腰直角三角形,同理△AOF2也是等腰直角三角形,
∴△F1AF2也是等腰直角三角形,
∴|F1A|=|F2A|=
| 6 |
∴∠BAF2=90°,
设|BF1|=x,根据椭圆定义,x+|BF2|=2a=2
| 6 |
根据勾股定理,AB2+AF22=BF22,
(
| 6 |
| 6 |
| 6 |
∴x=
| ||
| 3 |
∴S△ABF2=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| ||
| 3 |
| 6 |
故选D.
点评:本题以椭圆的标准方程为载体,考查椭圆焦点三角形的面积,解题的关键是求出判断出∠BAF2=90°.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
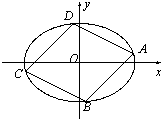 (2009•海淀区二模)如图,四边形ABCD的顶点都在椭圆
(2009•海淀区二模)如图,四边形ABCD的顶点都在椭圆