题目内容
(本小题满分12分)
集合A={(x,y)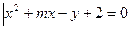 },集合B={(x,y)
},集合B={(x,y)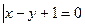 ,且0
,且0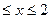 },又A
},又A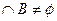 ,求实数m的取值范围
,求实数m的取值范围
集合A={(x,y)
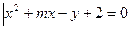 },集合B={(x,y)
},集合B={(x,y)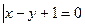 ,且0
,且0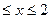 },又A
},又A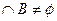 ,求实数m的取值范围
,求实数m的取值范围解:由A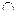 B
B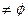 知方程组
知方程组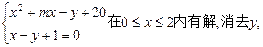
得x2+(m-1)x="0" 在0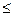 x
x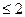 内有解,
内有解,
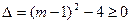 即m
即m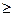 3或m
3或m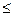 -1.
-1.
若m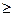 3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根.
3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根.
若m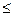 -1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内.
-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内.
因此{m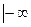 <m
<m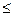 -1}.
-1}.
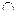 B
B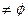 知方程组
知方程组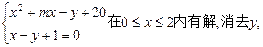
得x2+(m-1)x="0" 在0
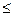 x
x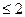 内有解,
内有解, 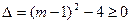 即m
即m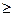 3或m
3或m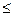 -1.
-1.若m
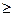 3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根.
3,则x1+x2=1-m<0,x1x2=1,所以方程只有负根.若m
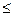 -1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内.
-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内.因此{m
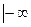 <m
<m -1}.
-1}.略

练习册系列答案
相关题目
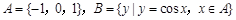 ,则
,则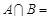 ( )
( )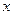 的不等式
的不等式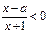 的解集为
的解集为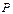 ,不等式
,不等式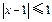 的解集为
的解集为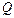 .
.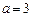 ,求集合
,求集合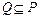 ,求正数
,求正数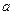 的取值
的取值 范围.
范围.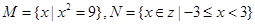 ,则
,则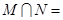 ( )
( )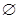
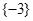
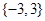
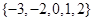
 ,则
,则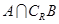 等( )
等( )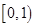
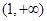
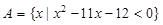 ,集合
,集合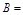 {
{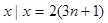 ,
,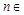 Z},则
Z},则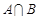 等于( )
等于( )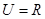 ,集合
,集合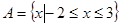 ,
,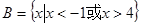 ,那么集合
,那么集合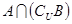 等于
等于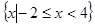
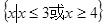

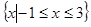
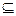 ∁RB,求实数m的取值范围.
∁RB,求实数m的取值范围.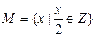 ,
,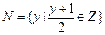 ,则
,则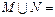 ( )
( )