题目内容
 (2009北京卷文)(本小题共14分)
(2009北京卷文)(本小题共14分)
如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面![]() ;
;
(Ⅱ)当![]() 且E为PB的中点时,求AE与
且E为PB的中点时,求AE与
平面PDB所成的角的大小.
【解法1】本题主要考查直线和平面垂直、平面与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力.
(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵![]() ,
,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面![]() .
.
(Ⅱ)设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∴O,E分别为DB、PB的中点,
∴OE//PD,![]() ,又∵
,又∵![]() ,
,
∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,![]() ,
,
∴![]() ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为![]() .
.
【解法2】如图,以D为原点建立空间直角坐标系![]() ,
,
设![]()
则![]() ,
,
(Ⅰ)∵![]() ,
,
∴![]() ,
,
∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面![]() .
.
(Ⅱ)当![]() 且E为PB的中点时,
且E为PB的中点时,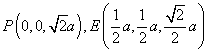 ,
,
设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵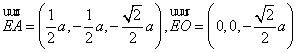 ,
,
∴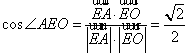 ,
,
∴![]() ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为![]() .
.

练习册系列答案
相关题目