题目内容
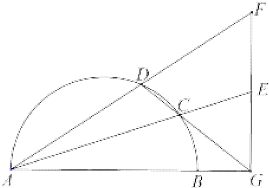 如图,在△AGF中,∠AGF是直角,B是线段AG上一点,以AB为直径的半圆交AF于D,连接DG交半圆于点C,延长AC交FG于E.
如图,在△AGF中,∠AGF是直角,B是线段AG上一点,以AB为直径的半圆交AF于D,连接DG交半圆于点C,延长AC交FG于E.(I)求证D、C、E、F四点共圆;
(II)若
| GE |
| GB |
| 3 |
| 2 |
| 2•GA |
| GF |
分析:(Ⅰ)连接BC,通过AB是直径,∠AGF是直角,推出E、B、C、G四点共圆,利用圆周角相等∠CEG=∠CDF,证明D、C、E、F四点共圆;
(Ⅱ)利用相交弦定理,以及已知条件直接推出
的值即可.
(Ⅱ)利用相交弦定理,以及已知条件直接推出
| 2•GA |
| GF |
解答:解:(Ⅰ)证明:连接BC,因为AB是直径,所以∠ACB=90°,
∵∠AGF是直径,∴E、B、C、G四点共圆,
∴∠ABC=∠CEG.
∵A、B、C、D四点共圆.∴∠ABC=∠CDF,
∴∠CEG=∠CDF,即D、C、E、F四点共圆;
(Ⅱ)由(Ⅰ)知D、C、E、F四点共圆,∴CE•GF=GC•GD,
又∵A、B、C、D四点共圆,∴GB•GA=GC•GD,∴GE•GF=GB•GA,
即
=
,
=
,
∴
=3.
∵∠AGF是直径,∴E、B、C、G四点共圆,
∴∠ABC=∠CEG.
∵A、B、C、D四点共圆.∴∠ABC=∠CDF,
∴∠CEG=∠CDF,即D、C、E、F四点共圆;
(Ⅱ)由(Ⅰ)知D、C、E、F四点共圆,∴CE•GF=GC•GD,
又∵A、B、C、D四点共圆,∴GB•GA=GC•GD,∴GE•GF=GB•GA,
即
| GA |
| GF |
| GE |
| GB |
| GE |
| GB |
| 3 |
| 2 |
∴
| 2•GA |
| GF |
点评:本题考查四点共圆的判断方法,相交弦定理的应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
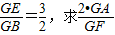 的值.
的值.
 的值.
的值.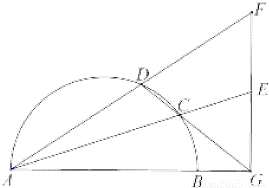
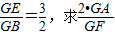 的值.
的值.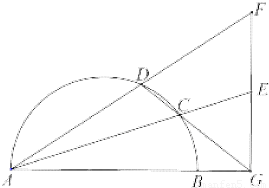
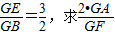 的值.
的值.