题目内容
设随机变量ξ～N（μ，σ2），且方程x2+4x+ξ=0无实根的概率为
，则μ的值是（ ）
| 1 |
| 2 |
| A、8 | B、6 | C、4 | D、2 |
分析：根据题中条件：“方程x2+4x+ξ=0无实根”得△＜0，再结合正态分布的图象规律即可求得μ的值．
解答：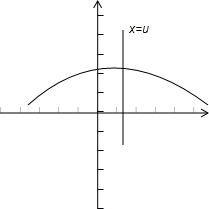
解：∵方程x2+4x+ξ=0无实根
∴得△＜0．
∴ξ＞4，
结合正态分布的图象，
它在x＞μ时的概率为
，故μ=4
故选C．
解：∵方程x2+4x+ξ=0无实根∴得△＜0．
∴ξ＞4，
结合正态分布的图象，
它在x＞μ时的概率为
| 1 |
| 2 |
故选C．
点评：本题主要考查正态分布的规律，正态分布涉及到连续型随机变量的分布密度，是概率统计中最重要的一种分布，也是自然界最常见的一种分布．
练习册系列答案
寒假学与练系列答案
相关题目
设随机变量X～N（3，?2），则P（X≤3）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|