题目内容
某校高一年级共有学生320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查,根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40, 50),⑥[50,60),⑦[60,70],得到频率分布直方图如图,已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人。

(1)求n的值;
(2)若高一全体学生平均每天晚自习自主支配学习时问少于45分钟,则学校需要减少作业量,根据以上抽样调查数据,学校是否需要减少作业量?(注:统计方法中,同一组数据常用该组区间的中点值作为代表)。
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7 名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人,求第3组中至少有一名学生被选聘为学情调查联系人的概率。
(2)若高一全体学生平均每天晚自习自主支配学习时问少于45分钟,则学校需要减少作业量,根据以上抽样调查数据,学校是否需要减少作业量?(注:统计方法中,同一组数据常用该组区间的中点值作为代表)。
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7 名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人,求第3组中至少有一名学生被选聘为学情调查联系人的概率。
解:(1)由频率分布直方图知第1组和第2组的频率分别是0.02 和0.06
则n×(0.02+0.06)=4,解得n=50。
(2)设第i组的频率和频数分别是Pi和xi,
由图知P1=0.02,P2=0.06,P3=0.3,P4=0.4,P5=0.12,P6=0.08,P7=0.02,
则由xi=50×Pi
可得x1=1,x2=3,x3=15,x4=20,x5=6,x6=4,x7=1
则高一学生每天平均自主支配时间是
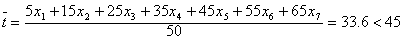
则学校应该想办法适当减少教师的作业布置量。
(3)第3组和第4组的频数分别是15和20,
用分层抽样的方法抽取7人,则第3组应抽 (人),
(人),
第4组应抽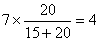 (人)
(人)
设第3组中被抽到的3名学生分别是甲、乙、丙,第4组被抽到的4 名学生分别是a,b,c,d
则从7人中抽取2人的基本事件空间Ω={(甲,乙),(甲,丙),(甲,a),(甲,b),(甲,c),(甲,d),(乙,丙),(乙,a),(乙,b).(乙,c),(乙,d),(丙,a),(丙,b),(丙,c),(丙,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)},共21个基本事件
其中事件A=“第3组中至少有1人被选聘”共含有15个基本事件,
则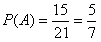 ,则第3组中至少有1人被选聘的概率是
,则第3组中至少有1人被选聘的概率是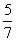 。
。
则n×(0.02+0.06)=4,解得n=50。
(2)设第i组的频率和频数分别是Pi和xi,
由图知P1=0.02,P2=0.06,P3=0.3,P4=0.4,P5=0.12,P6=0.08,P7=0.02,
则由xi=50×Pi
可得x1=1,x2=3,x3=15,x4=20,x5=6,x6=4,x7=1
则高一学生每天平均自主支配时间是
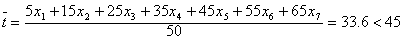
则学校应该想办法适当减少教师的作业布置量。
(3)第3组和第4组的频数分别是15和20,
用分层抽样的方法抽取7人,则第3组应抽
 (人),
(人),第4组应抽
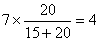 (人)
(人)设第3组中被抽到的3名学生分别是甲、乙、丙,第4组被抽到的4 名学生分别是a,b,c,d
则从7人中抽取2人的基本事件空间Ω={(甲,乙),(甲,丙),(甲,a),(甲,b),(甲,c),(甲,d),(乙,丙),(乙,a),(乙,b).(乙,c),(乙,d),(丙,a),(丙,b),(丙,c),(丙,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)},共21个基本事件
其中事件A=“第3组中至少有1人被选聘”共含有15个基本事件,
则
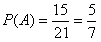 ,则第3组中至少有1人被选聘的概率是
,则第3组中至少有1人被选聘的概率是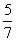 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.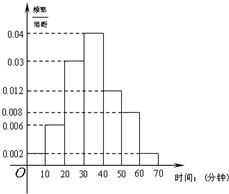 某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
