题目内容
已知A,B,C是△ABC的三个内角,且向量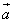 =cos
=cos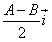 +
+ sin
sin 的模长为|
的模长为|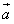 |=
|=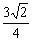 ,其中
,其中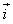 ,
,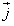 分别是平面直角坐标系x轴、y轴上的单位向量。
分别是平面直角坐标系x轴、y轴上的单位向量。
(1)求证:tanAtanB是定值;
(2)求tan(A+B)的最小值。
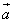 =cos
=cos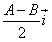 +
+ sin
sin 的模长为|
的模长为|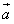 |=
|=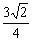 ,其中
,其中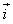 ,
,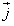 分别是平面直角坐标系x轴、y轴上的单位向量。
分别是平面直角坐标系x轴、y轴上的单位向量。(1)求证:tanAtanB是定值;
(2)求tan(A+B)的最小值。
(1)证明:由题意,得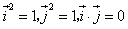 ,
,
则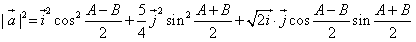
=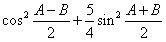
=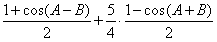 ,
,

则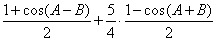 =
= ,
,
即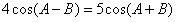 ,
,
∴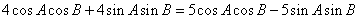 ,
,
 ,
,
 ,
,
即 。
。
所以tanAtanB是定值。
(2)解:由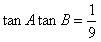 >0,且A,B,C是△ABC的三个内角,
>0,且A,B,C是△ABC的三个内角,
知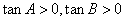 ,
,
则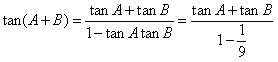
=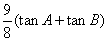
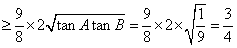 ,
,
当且仅当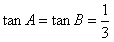 时,tan(A+B)的最小值为
时,tan(A+B)的最小值为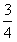 。
。
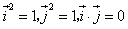 ,
,则
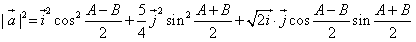
=
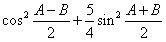
=
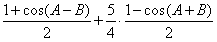 ,
,
则
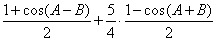 =
= ,
,即
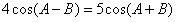 ,
,∴
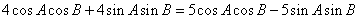 ,
, ,
, ,
,即
 。
。所以tanAtanB是定值。
(2)解:由
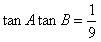 >0,且A,B,C是△ABC的三个内角,
>0,且A,B,C是△ABC的三个内角,知
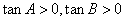 ,
,则
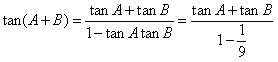
=
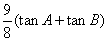
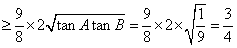 ,
,当且仅当
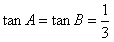 时,tan(A+B)的最小值为
时,tan(A+B)的最小值为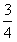 。
。
练习册系列答案
相关题目
 β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;
β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;