题目内容
已知α为第二象限角,则
+
的值是( )
| 2sinα | ||
|
| ||
| cosα |
分析:根据α为第二象限角,结合同角三角函数的平方关系,得出
=sinα,
=-cosα.由此代入题中式子进行化简,即可算出所求式子的值.
| 1-cos2α |
| 1-sin2α |
解答:解:∵α为第二象限角,
∴sinα>0且cosα<0
由此可得
=|sinα|=sinα,
=|cosα|=-cosα
∴
+
=
+
=2-1=1
故选:C
∴sinα>0且cosα<0
由此可得
| 1-cos2α |
| 1-sin2α |
∴
| 2sinα | ||
|
| ||
| cosα |
| 2sinα |
| sinα |
| -cosα |
| cosα |
故选:C
点评:本题给出α为第二象限角,要我们化简一个三角函数式子并求值,着重考查了三角函数的定义和同角三角函数的关系等知识,属于基础题.

练习册系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求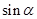 和
和 及
及 的值.
的值.