题目内容
若函数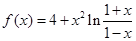 在区间
在区间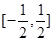 上的最大值与最小值分别为
上的最大值与最小值分别为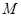 和
和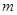 ,则
,则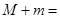 .
.
【答案】
8
【解析】
试题分析: 法一、令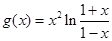 则
则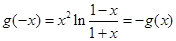 所以
所以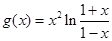 是奇函数
是奇函数
令 则在
则在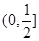 上
上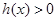 且递增,又
且递增,又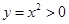 且递增
且递增
所以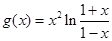 在
在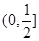 递增
递增
又因为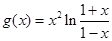 是奇函数,所以
是奇函数,所以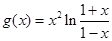 在
在 上递增,
上递增,
从而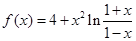 在区间
在区间 上递增
上递增
所以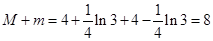
法二、
当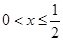 时
时 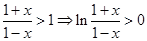 ,
,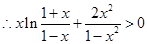
当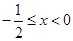 时
时 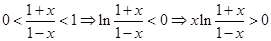 ,又
,又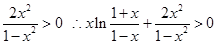
即当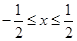 时,
时,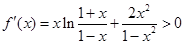
考点:1、导数的基本运算;2、函数的最大值最小值.

练习册系列答案
相关题目
 在区间
在区间 上的最大值是最小值的
上的最大值是最小值的 倍,则
倍,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 在区间
在区间 上的最大值是最小值的
上的最大值是最小值的 倍,则
倍,则 的值为( )
的值为( )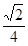 B.
B.  C.
C.  D.
D. 
 在区间
在区间 上的最大值为6,
上的最大值为6, 的对称中心;
的对称中心; 轴的对称图象得函数
轴的对称图象得函数 的图象,再把
的图象,再把 个单位得
个单位得 的图象,求函数
的图象,求函数 ,若函数
,若函数 在区间
在区间 上
上 ,最小值为
,最小值为 ,令
,令 .
.  的函数表达式;
的函数表达式; 上的单调性,并求出
上的单调性,并求出 在区间
在区间 上的最大值为2,则它在该区间上的最小值为( )
上的最大值为2,则它在该区间上的最小值为( ) B.7 C.10 D.
B.7 C.10 D.