题目内容
已知函数 ,下列命题中不正确的是( )
,下列命题中不正确的是( )
A. 的图象关于直线 的图象关于直线 对称 对称 |
B. 的图象关于点 的图象关于点 成中心对称 成中心对称 |
C. 在区间 在区间 上单调递增 上单调递增 |
D. 在区间 在区间 上的最大值是 上的最大值是 ,最小值是 ,最小值是 |
B
解析试题分析:根据题意,由于函数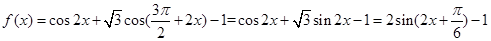 ,那么可知,当
,那么可知,当 时函数取得最值,因此可知为对称轴方程,成立。当把点
时函数取得最值,因此可知为对称轴方程,成立。当把点 代入可知函数值没有取得-1,故错误,不是对称中心,对于选项C,根据
代入可知函数值没有取得-1,故错误,不是对称中心,对于选项C,根据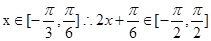 满足正弦函数的增区间,因此成立,对于选项D,由于
满足正弦函数的增区间,因此成立,对于选项D,由于 在区间
在区间 上,可知
上,可知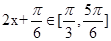 的最大值是
的最大值是 ,最小值是
,最小值是 成立,故选B.
成立,故选B.
考点:三角函数的性质
点评:解决的关键是对于三角函数的性质的熟练运用,属于常规试题,容易得分。

练习册系列答案
相关题目
若 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知 是函数
是函数 的一条对称轴,且
的一条对称轴,且 的最大值为
的最大值为 ,则函数
,则函数
| A.最大值是4,最小值是0 | B.最大值是2,最小值是-2 |
| C.最小值不可能是-4 | D.最大值可能是0 |
已知 是第二象限的角,且
是第二象限的角,且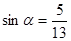 ,则
,则
 的值是( )
的值是( )
A. | B. | C. | D. |
已知函数 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是( )
的解析式是( )
A. | B.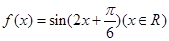 |
C. | D. |
时间经过2h,时针转过的角是( )
A. | B. | C.2π | D. π π |
函数 的图像的一条对称轴方程是( )
的图像的一条对称轴方程是( )
A. | B.  | C.  | D. |
将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在[
在[ ]上为增函数,则
]上为增函数,则 的最大值为
的最大值为
| A.4 | B.3 | C.2 | D.1 |
 的图象与x轴交于点A,过点A的直线
的图象与x轴交于点A,过点A的直线 与函数的图象交于B、C两点,则
与函数的图象交于B、C两点,则 ( )
( ) B.
B. C.
C. D.
D.