题目内容
F(c,0)是椭圆
+
=1(a>b>0)的一个焦点,F与椭圆上点的距离的最大值为m,最小值为n,则椭圆上与点F距离为
的点是______.
| x2 |
| a2 |
| y2 |
| b2 |
| m+n |
| 2 |
因为F(c,0)是椭圆
+
=1(a>b>0)的一个焦点,
F与椭圆上点的距离的最大值为m,最小值为n,所以m=a+c,n=a-c,
所以
=
=a,
所以椭圆上与点F距离为
的点是短轴的端点,即(0,±b).
故答案为:(0,±b).
| x2 |
| a2 |
| y2 |
| b2 |
F与椭圆上点的距离的最大值为m,最小值为n,所以m=a+c,n=a-c,
所以
| m+n |
| 2 |
| a+c+a-c |
| 2 |
所以椭圆上与点F距离为
| m+n |
| 2 |
故答案为:(0,±b).

练习册系列答案
相关题目
 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆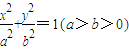 的右焦点,以坐标原点O为圆心,a为半径作圆P,过F垂直于x轴的直线与圆P交于A,B两点,过点A作圆P的切线交x轴于点M.若直线l过点M且垂直于x轴,则直线l的方程为 ;若|OA|=|AM|,则椭圆的离心率等于 .
的右焦点,以坐标原点O为圆心,a为半径作圆P,过F垂直于x轴的直线与圆P交于A,B两点,过点A作圆P的切线交x轴于点M.若直线l过点M且垂直于x轴,则直线l的方程为 ;若|OA|=|AM|,则椭圆的离心率等于 .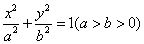 的右焦点,以坐标原点O为圆心,A为半径作圆P,过F垂直于x轴的直线与圆P交于A,B两点,过点A作圆P的切线交x轴于点M。若直线l过点M且垂直于x轴,则直线l的方程为
;若|OA|=|AM|,则椭圆的离心率等于
。
的右焦点,以坐标原点O为圆心,A为半径作圆P,过F垂直于x轴的直线与圆P交于A,B两点,过点A作圆P的切线交x轴于点M。若直线l过点M且垂直于x轴,则直线l的方程为
;若|OA|=|AM|,则椭圆的离心率等于
。