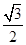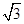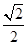题目内容
在 中,
中,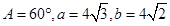 ,则
,则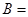 ( )
( )
A.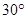 | B.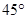 | C.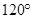 | D.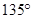 |
B
解析试题分析:由正弦定理 可知
可知 即
即 ,而
,而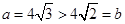 ,且
,且 均为三角形的内角,故
均为三角形的内角,故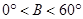 ,所以
,所以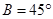 ,故选B.
,故选B.
考点:1.三角形的边角关系;2.正弦定理.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
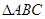 中,
中,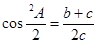 ,则
,则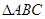 形状是( )
形状是( )
| A.正三角形 | B.直角三角形 |
| C.等腰三角形或直角三角形 | D.等腰直角三角形 |
在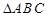 中,角
中,角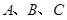 所对的边分别为
所对的边分别为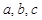 ,若
,若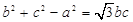 ,且
,且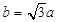 ,则下列关系一定不成立的是( )
,则下列关系一定不成立的是( )
A.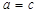 | B.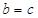 | C.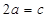 | D.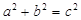 |
△ABC中, ∠A,∠B,∠C所对的边分别为a, b, c.若 ,∠C=
,∠C= , 则边 c 的值等于( )
, 则边 c 的值等于( )
| A.5 | B.13 | C.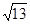 | D.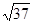 |
在△ABC中,角A,B,C的对边为 ,若
,若 ,则角A= ( )
,则角A= ( )
| A.30° | B.30°或105° | C.60° | D.60°或120° |
在△ABC中,角A,B,C所对的边长分别为a,b,c,若C=120°,c= a,则( )
a,则( )
| A.a>b |
| B.a<b |
| C.a=b |
| D.a与b的大小关系不能确定 |
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( ).
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |
在锐角△ABC中,BC=1,B=2A,则AC的取值范围是( ).
| A.[-2,2] | B.[0,2] | C.(0,2] | D.( , ,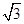 ) ) |