题目内容
若f(x)=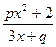 是奇函数,且f(2)=
是奇函数,且f(2)=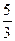 .
.
(1)、求实数p、q的值;(2)判断f(x)在(-∝,-1)的单调性,并加以证明。
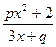 是奇函数,且f(2)=
是奇函数,且f(2)=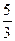 .
.(1)、求实数p、q的值;(2)判断f(x)在(-∝,-1)的单调性,并加以证明。
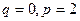
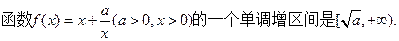
(1)解:∵f(x)是奇函数,f(2)=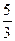 ∴f(-2)=
∴f(-2)=
又f(x)=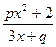 ,故有
,故有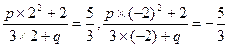
解得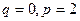 故
故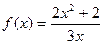
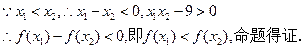
(2)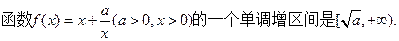
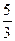 ∴f(-2)=
∴f(-2)=
又f(x)=
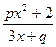 ,故有
,故有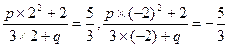
解得
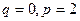 故
故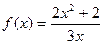
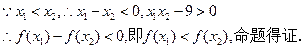
(2)
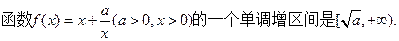

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
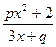 是奇函数,且f(2)=
是奇函数,且f(2)=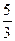 .
.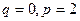
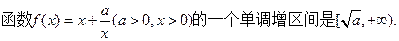
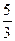 ∴f(-2)=
∴f(-2)=
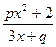 ,故有
,故有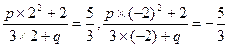
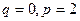 故
故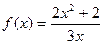
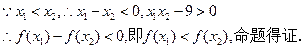
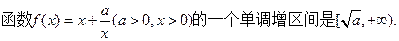

 阅读快车系列答案
阅读快车系列答案