题目内容
下面是关于圆锥曲线的四个命题:
①抛物线y2=2px的准线方程为y=-
;
②设A、B为两个定点,a为正常数,若
+
=2a,则动点P的轨迹为椭圆;
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④平面内与定点A(5,0)的距离和定直线l:x=
的距离之比为
的点的轨迹方程为
-
=1.其中所有真命题的序号为
①抛物线y2=2px的准线方程为y=-
| p |
| 2 |
②设A、B为两个定点,a为正常数,若
| |PA| |
| |PB| |
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④平面内与定点A(5,0)的距离和定直线l:x=
| 16 |
| 5 |
| 5 |
| 4 |
| x2 |
| 16 |
| y2 |
| 9 |
③④
③④
.分析:对于①利用抛物线的标准形式即可得到其准线方程.对于②利用椭圆的定义即可进行判断;对于③结合椭圆和双曲线的离心率的取值范围即可求解;对于④,利用动点P到定点A(5,0)的距离与到定直线x=
的距离的比是
可得方程,化简由此能求出轨迹M的方程.
| 16 |
| 5 |
| 5 |
| 4 |
解答:解:①抛物线y2=2px的准线方程为x=-
;故①错;
②根据椭圆的定义,只有当P到两定点A、B距离之和大于|AB|即2a>|
|+|
|时,动点P的轨迹为椭圆.②假命题
③方程2x2-5x+2=0的两根是x=
<1,可作为椭圆的离心率;x=2>1可双曲线的离心率.③真命题
对于④,由题意,设P(x,y),则
=
,化简得轨迹方程是
-
=1,正确.
故答案为:③④.
| p |
| 2 |
②根据椭圆的定义,只有当P到两定点A、B距离之和大于|AB|即2a>|
| PA |
| PB |
③方程2x2-5x+2=0的两根是x=
| 1 |
| 2 |
对于④,由题意,设P(x,y),则
| (x-5)2+y2 | ||
(x-
|
| 25 |
| 16 |
| x2 |
| 16 |
| y2 |
| 9 |
故答案为:③④.
点评:本题考查了椭圆、双曲线的定义标准方程、简单的几何性质等基础知识,考查轨迹方程的求法,属于基础题.

练习册系列答案
相关题目
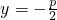 ;
;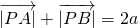 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;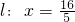 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为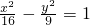 .其中所有真命题的序号为________.
.其中所有真命题的序号为________.