题目内容
已知x>1,y>1且2logxy-2logyx+3=0,记M=x2-4y2.
(1)求出M关于x的函数解析式f(x),并求其值域;
(2)解关于t的方程f(t2+2)=f(3t).
解:(1)设n=logxy,
因为x>1,y>1,所以n>0.
因为2logxy-2logyx+3=0,
所以可得2n2+3n-2=0,解得:n= 或者n=-2(舍去),
或者n=-2(舍去),
所以logxy= ,即y2=x,
,即y2=x,
所以M=x2-4y2=x2-4x,即f(x)=x2-4x,(x>1),
根据二次函数的有关性质可得:f(x)∈[-3,+∞),即值域为[-3,+∞).
(2)由(1)并且结合二次函数的性质可得:t2+2=3t或者(t2+2)+(3t)=4,
解得t=1,t=2,t=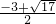 ,t=
,t=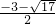 .
.
又因为f(x)=x2-4x,(x>1),
所以t2+2≥-3,并且3t≥-3,解得:t≥-1.
所以方程的解为t=1,t=2,t=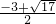 .
.
分析:(1)设n=logxy,根据题意可得n>0,以及得到2n2+3n-2=0,求出n的数值即可得到y2=x,进而得到函数f(x)的解析式,再根据二次函数的性质得到答案.
(2)结合二次函数的性质可得:t2+2=3t或者(t2+2)+(3t)=4,即可求出t的值,再根据函数的定义域得到方程的解.
点评:解决此类问题的关键是熟练掌握一元二次方程的解法与一元二次函数的有关性质,以及对数的有关运算,此题属于中档题型.
因为x>1,y>1,所以n>0.
因为2logxy-2logyx+3=0,
所以可得2n2+3n-2=0,解得:n=
 或者n=-2(舍去),
或者n=-2(舍去),所以logxy=
 ,即y2=x,
,即y2=x,所以M=x2-4y2=x2-4x,即f(x)=x2-4x,(x>1),
根据二次函数的有关性质可得:f(x)∈[-3,+∞),即值域为[-3,+∞).
(2)由(1)并且结合二次函数的性质可得:t2+2=3t或者(t2+2)+(3t)=4,
解得t=1,t=2,t=
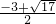 ,t=
,t=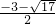 .
.又因为f(x)=x2-4x,(x>1),
所以t2+2≥-3,并且3t≥-3,解得:t≥-1.
所以方程的解为t=1,t=2,t=
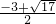 .
.分析:(1)设n=logxy,根据题意可得n>0,以及得到2n2+3n-2=0,求出n的数值即可得到y2=x,进而得到函数f(x)的解析式,再根据二次函数的性质得到答案.
(2)结合二次函数的性质可得:t2+2=3t或者(t2+2)+(3t)=4,即可求出t的值,再根据函数的定义域得到方程的解.
点评:解决此类问题的关键是熟练掌握一元二次方程的解法与一元二次函数的有关性质,以及对数的有关运算,此题属于中档题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 x>1,y>1且xy=16,则log2x?log2y( )
| A、有最大值2 | B、等于4 | C、有最小值3 | D、有最大值4 |