题目内容
已知点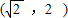 在幂函数f(x)的图象上,点
在幂函数f(x)的图象上,点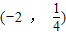 在幂函数g(x)的图象上.
在幂函数g(x)的图象上.(1)求函数f(x),g(x)的解析式;
(2)判断函数g(x)的单调性并用定义证明;
(3)问x为何值时有f(x)≤g(x).
【答案】分析:(1)求函数f(x),g(x)的解析式,由于已知两函数是幂函数,故可用待定系数法设出两函数的解析式,代入点的坐标求出函数的解析式.
(2)由定义进行证明即可;
由于两个函数在第一象限一个是减函数一个是增函数,故可令两者相等,解出它们的交点坐标,再由函数的单调性得出f(x)≤g(x)的解集,由于两函数都是偶函数,可由对称性得出函数在(-∞,0)上的解集,取两者的并集即得不等式f(x)≤g(x)的解集,即得所求的x的取值范围.
解答:解:(1)由题易得f(x)=x2 ,g(x)=x-2
(2)g(x)在(0,+∞)上为减函数,在(-∞,0)上为增函数
证明:任取x1<x2<0,有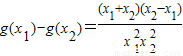
∵x1+x2<0,x2-x1>0,x12x22>0
∴g(x1)-g(x2)<0
∴g(x)在(0,+∞)上为增函数.
任取0<x1<x2,有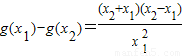
∵x2+x1>0,x2-x1>0,x12x22>0
∴g(x1)>g(x2)
∴g(x)在(0,+∞)上是减函数.
(3)当x>1或x<1时,f(x)≤g(x),证明如下
由(1),两函数都是偶函数,先研究x>0时满足f(x)≤g(x)的x的取值范围.
令x2 =x-2,解得x=1,又f(x)=x2 在(0,+∞)上是增函数,g(x)=x-2在(0,+∞)上是减函数,故可得f(x)≤g(x)的x的取值范围是x≤1
由两函数的解析式知,此两函数都是偶函数,故当x<0时,f(x)≤g(x)的x的取值范围是x≥-1
综上当-1≤x≤1时,f(x)≤g(x)
点评:本题考查幂函数单调性、奇偶性及其应用,解题的关键是熟练掌握幂函数的性质,且能根据其性质进行运算,本题考查到了函数的单调性的证明方法定义法,要注意证明的步骤
(2)由定义进行证明即可;
由于两个函数在第一象限一个是减函数一个是增函数,故可令两者相等,解出它们的交点坐标,再由函数的单调性得出f(x)≤g(x)的解集,由于两函数都是偶函数,可由对称性得出函数在(-∞,0)上的解集,取两者的并集即得不等式f(x)≤g(x)的解集,即得所求的x的取值范围.
解答:解:(1)由题易得f(x)=x2 ,g(x)=x-2
(2)g(x)在(0,+∞)上为减函数,在(-∞,0)上为增函数
证明:任取x1<x2<0,有
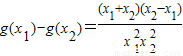
∵x1+x2<0,x2-x1>0,x12x22>0
∴g(x1)-g(x2)<0
∴g(x)在(0,+∞)上为增函数.
任取0<x1<x2,有
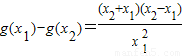
∵x2+x1>0,x2-x1>0,x12x22>0
∴g(x1)>g(x2)
∴g(x)在(0,+∞)上是减函数.
(3)当x>1或x<1时,f(x)≤g(x),证明如下
由(1),两函数都是偶函数,先研究x>0时满足f(x)≤g(x)的x的取值范围.
令x2 =x-2,解得x=1,又f(x)=x2 在(0,+∞)上是增函数,g(x)=x-2在(0,+∞)上是减函数,故可得f(x)≤g(x)的x的取值范围是x≤1
由两函数的解析式知,此两函数都是偶函数,故当x<0时,f(x)≤g(x)的x的取值范围是x≥-1
综上当-1≤x≤1时,f(x)≤g(x)
点评:本题考查幂函数单调性、奇偶性及其应用,解题的关键是熟练掌握幂函数的性质,且能根据其性质进行运算,本题考查到了函数的单调性的证明方法定义法,要注意证明的步骤

练习册系列答案
相关题目
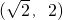 在幂函数f(x)的图象上,点
在幂函数f(x)的图象上,点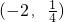 在幂函数g(x)的图象上.
在幂函数g(x)的图象上.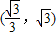 在幂函数f(x)的图象上,则f(x)是( )
在幂函数f(x)的图象上,则f(x)是( )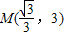 在幂函数f(x)的图象上,则f(x)的表达式为( )
在幂函数f(x)的图象上,则f(x)的表达式为( )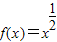
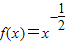
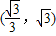 在幂函数f(x)的图象上,则f(x)是( )
在幂函数f(x)的图象上,则f(x)是( )