题目内容
(中坐标运算)已知向量a=(1,2),b=(3,2),且|(ka+b)-(a-3b)|=|ka+b|+|a-3b|,则实数k的值等于 .
【答案】分析:由题意a,b不共线,由已知等式|(ka+b)-(a-3b)|=|ka+b|+|a-3b|得ka+b与a-3b共线且方向相反,
利用向量坐标形式的共线的条件求解即可.
解答:解:由题意a,b不共线,由已知等式得ka+b与a-3b共线且方向相反,
当(ka+b)∥(a-3b)时,有ka+b=λ(a-3b)=λa-3λb,
得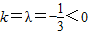 ,合题意.
,合题意.
∴实数k的值等于 .
.
点评:本题考查向量位置关系、向量的坐标形式的共线的条件的运用.由题意看出ka+b与a-3b位置关系是解题的关键,简化了运算.
利用向量坐标形式的共线的条件求解即可.
解答:解:由题意a,b不共线,由已知等式得ka+b与a-3b共线且方向相反,
当(ka+b)∥(a-3b)时,有ka+b=λ(a-3b)=λa-3λb,
得
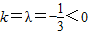 ,合题意.
,合题意.∴实数k的值等于
 .
.点评:本题考查向量位置关系、向量的坐标形式的共线的条件的运用.由题意看出ka+b与a-3b位置关系是解题的关键,简化了运算.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目